giúp em bài 4 với ạ,em cảm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



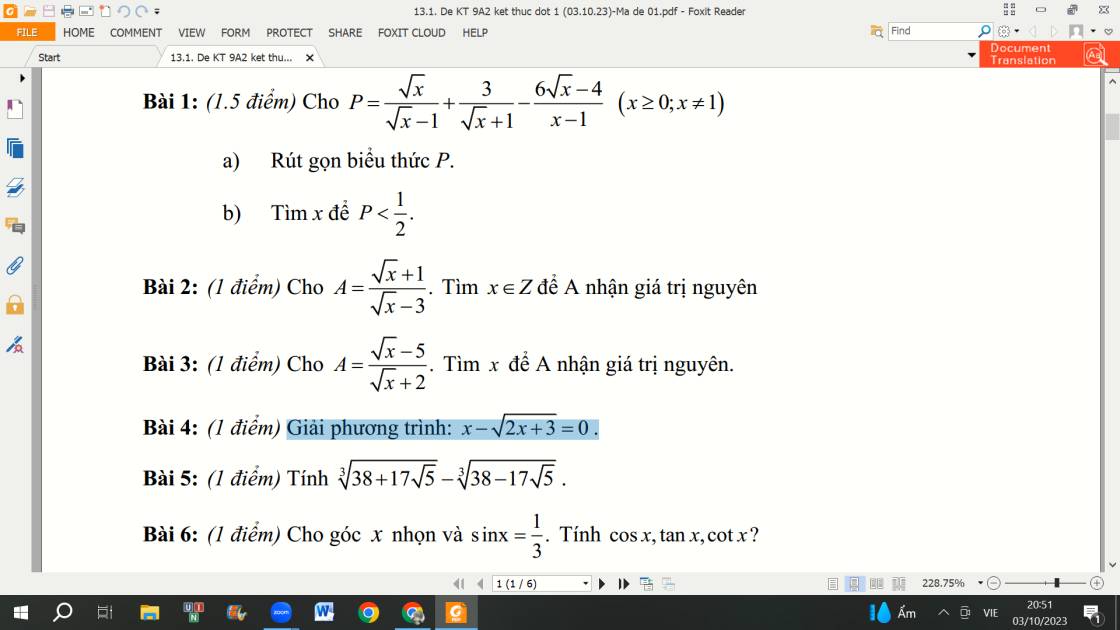
\(x-\sqrt{2x+3}=0\) \(ĐK:x\ge\dfrac{-3}{2}\)
\(\Leftrightarrow x=\sqrt{2x+3}\left(x\ge0\right)\)
\(\Leftrightarrow x^2=2x+3\)
\(\Leftrightarrow x^2-2x-3=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\left(TM\right)\\x=-1\left(KTM\right)\end{matrix}\right.\)
Vậy.........

a) \(m_S=m_B-m_{hh\left(bđ\right)}=29,55-15,15=14,4\left(g\right)\)
b) \(n_S=\dfrac{14,4}{32}=0,45\left(mol\right)\)
Kết tủa thu được là Ag2S
Bảo toàn S: \(n_{Ag_2S}=0,45\left(mol\right)\)
=> \(m_{Ag_2S}=0,45.248=111,6\left(g\right)\)

a) Ta có: AB//CD.
=>ABH=BDC (2 góc so le trong).
=> ∆AHB~∆BCD(g.g).
b) ∆ABD có : DB²=AB²+AD²( Định lý Pitago)
=> DB= 15(cm).
Ta có ∆ABH~∆BCD(cmt).
=>AH/BC=AD/BD.
Hay AH=9.12/15=7,2(cm).
c)Ta có ∆AHB~∆BCD cmt.
=> HBA=CBD. (1)
Ta lại có : CBD= ADH (AB//CD).(2)
Từ 1 và 2 => HAB=ADH.
=>∆DHA~∆AHB(g.g).
S∆DHA/S∆AHB=(AD/AB)²=9/16
d) từ câu (a) và (b) => ∆BCD~∆DHA.
Cm ∆DHA~∆MDA(g.g)
Từ đó suy ra ∆BDC~∆MDA.
Sau đó cm ∆BCD~∆ADC(g.g).
=> ∆MDA~∆ADC(g.g).
=>Ad/DC=DM/DC.
=>Đpcm.

a) Gọi số mol Zn, Al là a, b (mol)
=> 65a + 27b = 1,84 (1)
PTHH: Zn + 2HCl --> ZnCl2 + H2
a--------------->a----->a
2Al + 6HCl --> 2AlCl3 + 3H2
b-------------->b----->1,5b
=> 136a + 133,5b = 5,39 (2)
(1)(2) => a = 0,02 (mol); b = 0,02 (mol)
=> \(\left\{{}\begin{matrix}\%m_{Zn}=\dfrac{0,02.65}{1,84}.100\%=70,65\%\\\%m_{Al}=\dfrac{0,02.27}{1,84}.100\%=29,35\%\end{matrix}\right.\)
b) nH2 = a + 1,5b = 0,05 (mol)
=> VH2 = 0,05.22,4 = 1,12 (l)

\(a^3+b^3=\sqrt{\left(\sqrt{6}-\sqrt{2}\right)^2}-\dfrac{4\left(\sqrt{6}-\sqrt{2}\right)}{\left(\sqrt{6}+\sqrt{2}\right)\left(\sqrt{6}-\sqrt{2}\right)}\)
\(=\sqrt{6}-\sqrt{2}-\dfrac{4\left(\sqrt{6}-\sqrt{2}\right)}{4}=0\)
\(\Rightarrow a=-b\Rightarrow a^5+b^5=0\)

4:
1: S=1,2^2*3,14=4,5216m3
2:
a: góc ABC+góc ABF=180 độ
=>B,C,F thẳng hàng
góc CDF=góc CEF=90 độ
=>CDEF nội tiếp




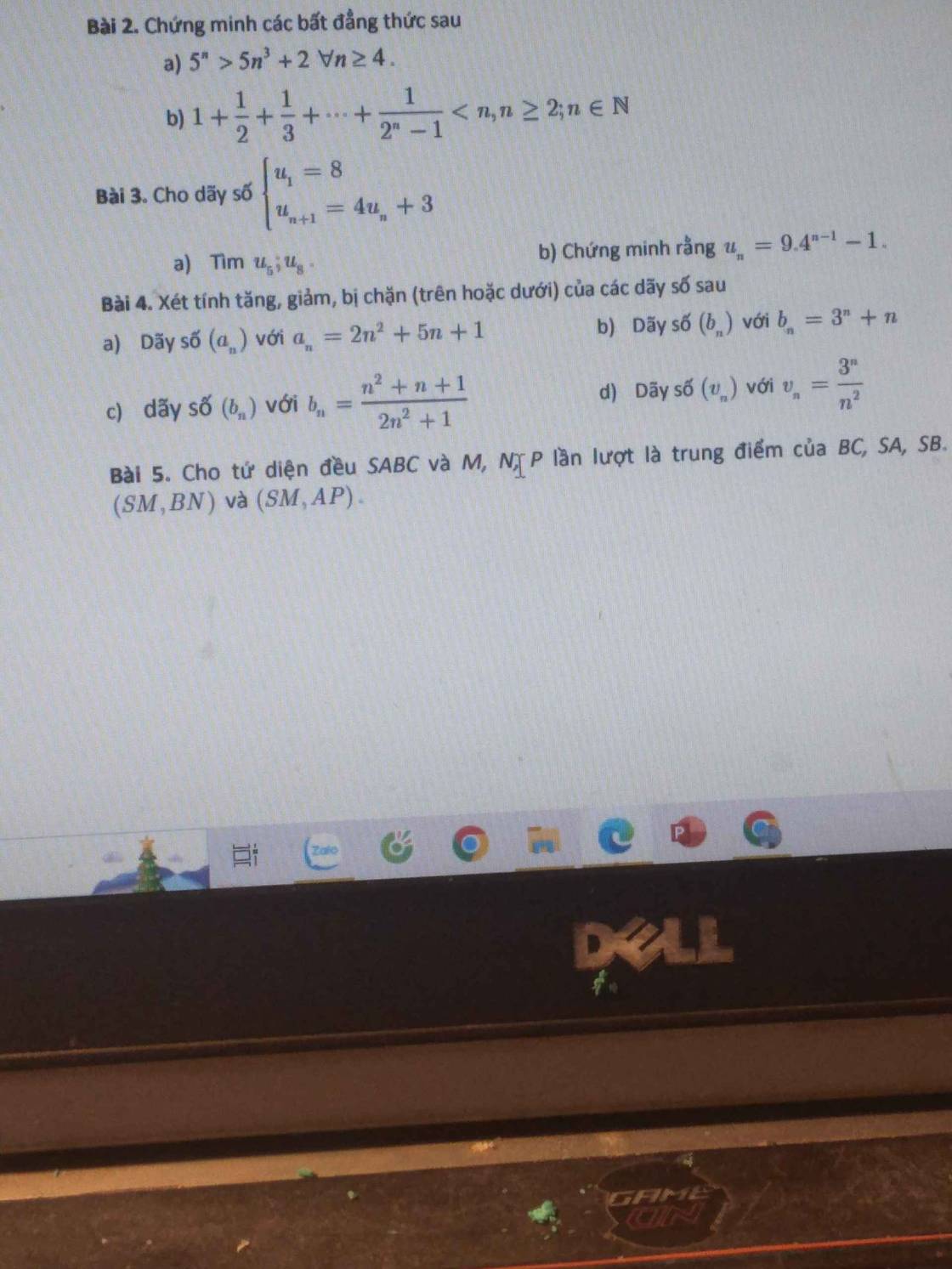 giúp em xét đãy số bị chặn của bài 4 với ạ. cần gấp ạ. Em cảm ơn ạ
giúp em xét đãy số bị chặn của bài 4 với ạ. cần gấp ạ. Em cảm ơn ạ
a: Ta có: \(A=\sin^21^0+\sin^22^0+...+\sin^288^0+\sin^289^0\)
\(=\left(\sin^21^0+\sin^289^0\right)+...+\sin^245^0\)
\(=1+1+...+1+\dfrac{1}{2}\)
\(=\dfrac{89}{2}\)