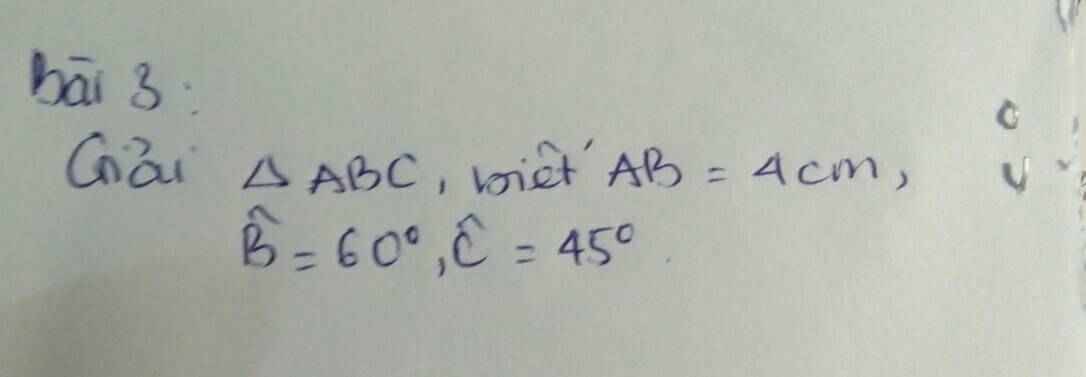mik đang càn gấp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 8 2021
Câu 1:
a: Để hàm số đồng biến thì m-5>0
hay m>5
b: Để hàm số nghịch biến thì m-5<0
hay m<5
N
9 tháng 9 2021
Tham khảo:
Dế Mèn trong tác phẩm "Bài học đường đời đầu tiên" hiện lên ngây thơ, tự tin, yêu đời nhưng cùng kiêu căng, hung hăng, hống hách với những cử chỉ khờ dại, việc làm thiếu suy nghĩ, gây tai hoạ cho kẻ khác. Những đặc điểm ấy của chú tuy là của một con dê mới lớn nhưng lại mang những nét tâm lý, những nết tốt, những ước mơ, những tật xấu thói hư, những thành công, những vấp ngã đầu đời quen thuộc của tuổi nhỏ chúng em hôm nay. Đọc Dế Mèn phiêu lưu ký ai không thấy thú vị dõi theo từng bước đường đầy những cảnh ngộ éo le, sinh động và hấp dẫn. Nhưng lý thú và bổ ích hơn nữa là những bài học mà nhà vần Tô Hoài đã giúp chúng ta rút ra được từ cuộc hành trình của chú dế mới lớn tuy có lúc đáng giận mà cũng thật là đáng yêu mến này.
11 tháng 9 2021
Bài 3:
a: Ta có: \(\widehat{DBE}=\widehat{ABE}\)
mà \(\widehat{ABE}=\widehat{DEB}\)
nên \(\widehat{DBE}=\widehat{DEB}\)
DM
1
AH
Akai Haruma
Giáo viên
12 tháng 8 2023
Lời giải:
a. Với $n$ nguyên khác -3, để $B$ nguyên thì:
$2n+9\vdots n+3$
$\Rightarrow 2(n+3)+3\vdots n+3$
$\Rightarrow 3\vdots n+3$
$\Rightarrow n+3\in\left\{\pm 1; \pm 3\right\}$
$\Rightarrow n\in\left\{-2; -4; 0; -6\right\}$
b.
$B=\frac{2n+9}{n+3}=\frac{2(n+3)+3}{n+3}=2+\frac{3}{n+3}$
Để $B_{\max}$ thì $\frac{3}{n+3}$ max
Điều này đạt được khi $n+3$ là số nguyên dương nhỏ nhất
Tức là $n+3=1$
$\Leftrightarrow n=-2$
c. Để $B$ min thì $\frac{3}{n+3}$ min
Điều này đạt được khi $n+3$ là số nguyên âm lớn nhất
Tức là $n+3=-1$
$\Leftrightarrow n=-4$
29 tháng 1 2022
\(S_{KNO_3}=\frac{m_{KNO_3}.100}{m_{H_2O}}=\frac{100.24}{80}=30g\)
10 tháng 11 2017
Có : 7^2012 = 7^4.503 = (7^4)^503 = (...1)^503 = ....1 ( số ...1 có gạch ngang trên đầu nha ) => 7^2012^2014 = (...1)^2014 = ...1
3^92 = 3^4.23 = (3^4)^23 = (....1)^23 = ....1 => 3^92^94 = (....1)^2014 = ...1
=> B = 1/2 . (....1 - ....1 ) = 1/2 . (....0)
=> B có tận cùng là 5 hoặc 0 => B chia hết cho 5 (ĐPCM)
MH
17 tháng 10 2023
Ta có:
\(\widehat{A}=180^o-60^o-45^o=75^o\)(tổng 3 góc trong tam giác)
Kẻ đường cao AH
\(sin60=\dfrac{AH}{AB}\)
\(\Rightarrow AH=sin60.4=2\sqrt{3}\)
\(sin45=\dfrac{AH}{AC}\)
\(\Rightarrow AC=\dfrac{2\sqrt{3}}{sin45}=2\sqrt{6}\)
\(BC=\sqrt{4^2-\left(2\sqrt{3}\right)^2}+\sqrt{\left(2\sqrt{6}\right)^2-\left(2\sqrt{3}\right)^2}=2+2\sqrt{3}\)
DH
1
30 tháng 9 2021
\(A=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{2}{x-1}\)
\(A=\dfrac{x+\sqrt{x}-2\sqrt{x}-2}{x-1}-\dfrac{x-\sqrt{x}+2\sqrt{x}-2}{x-1}-\dfrac{2}{x-1}\)
\(A=\dfrac{x-\sqrt{x}-2-x-\sqrt{x}+2-2}{x-1}\)
\(A=\dfrac{2\sqrt{x}-2}{x-1}\)
\(A=\dfrac{2\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{2}{\sqrt{x}+1}\)
b)
\(\dfrac{2}{\sqrt{x}+1}=-1\)
=>\(\sqrt{x}+1=-2\)
\(\sqrt{x}=-3\)
ko có x thỏa mãn
11 tháng 10 2021
#include <bits/stdc++.h>
using namespace std;
int main()
{
long long a,c,tam;
cin>>a>>c;
cout<<"a truoc khi doi la:"<<a<<endl;
cout<<"c truoc khi doi la:"<<c<<endl;
tam=a;
a=c;
c=tam;
cout<<"a sau khi doi la:"<<a<<endl;
cout<<"c sau khi doi la:"<<c<<endl;
return 0;
}
