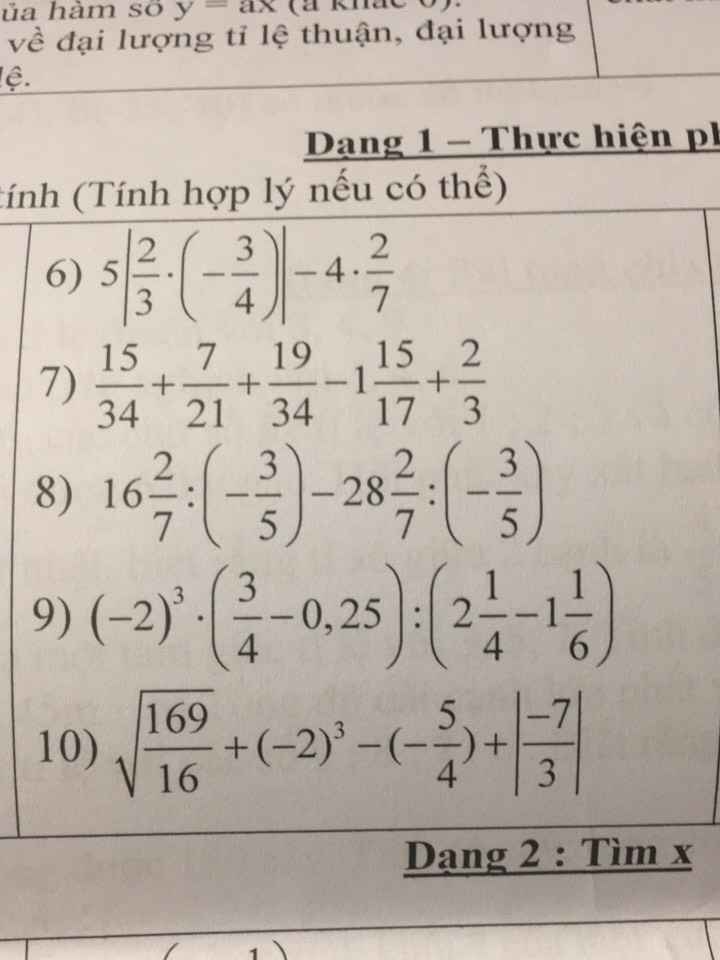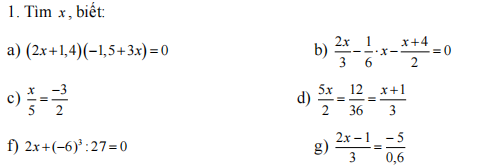K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
11 tháng 9 2021
Bài 3:
a: Ta có: \(\widehat{DBE}=\widehat{ABE}\)
mà \(\widehat{ABE}=\widehat{DEB}\)
nên \(\widehat{DBE}=\widehat{DEB}\)
DM
1
AH
Akai Haruma
Giáo viên
12 tháng 8 2023
Lời giải:
a. Với $n$ nguyên khác -3, để $B$ nguyên thì:
$2n+9\vdots n+3$
$\Rightarrow 2(n+3)+3\vdots n+3$
$\Rightarrow 3\vdots n+3$
$\Rightarrow n+3\in\left\{\pm 1; \pm 3\right\}$
$\Rightarrow n\in\left\{-2; -4; 0; -6\right\}$
b.
$B=\frac{2n+9}{n+3}=\frac{2(n+3)+3}{n+3}=2+\frac{3}{n+3}$
Để $B_{\max}$ thì $\frac{3}{n+3}$ max
Điều này đạt được khi $n+3$ là số nguyên dương nhỏ nhất
Tức là $n+3=1$
$\Leftrightarrow n=-2$
c. Để $B$ min thì $\frac{3}{n+3}$ min
Điều này đạt được khi $n+3$ là số nguyên âm lớn nhất
Tức là $n+3=-1$
$\Leftrightarrow n=-4$
DT
1
8 tháng 4 2022
Xét ΔCBD và ΔADB có
CD=AB
\(\widehat{CDB}=\widehat{ABD}\)
BD chung
Do đó: ΔCBD=ΔADB
Suy ra: \(\widehat{EBD}=\widehat{EDB}\)
hay ΔEBD cân tại E
Xét ΔOEB và ΔOED có
OE chung
EB=ED
OB=OD
Do đó: ΔOEB=ΔOED
Suy ra: \(\widehat{BOE}=\widehat{DOE}\)
hay OE là tia phân giác của góc xOy
LQ
Mình càn gấp nên mong mn giúp mình:((((
1
21 tháng 10 2021
a: \(\widehat{A}+\widehat{D}=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên AB//DC
29 tháng 12 2021
5: \(=\dfrac{1}{2}\cdot10-\dfrac{1}{2}=\dfrac{1}{2}\cdot9=\dfrac{9}{2}\)
NT
2
3 tháng 9 2023
`(2x - 1)^2 = 36`
`(2x - 1)^2 = 6^2` hoặc `(2x - 1)^2 = (-6)^2`
`2x - 1 = 6` hoặc `2x - 1 = -6`
`2x = 6 + 1` hoặc `2x = -6 + 1`
`2x = 7` hoặc `2x = -5`
`x = 7 : 2` hoặc `x = -5 : 2`
`x = 3,5` hoặc `x = -2,5`
ND
Nguyễn Đức Trí
VIP
3 tháng 9 2023
\(\left(2x-1\right)^2=36\)
\(\Rightarrow\left(2x-1\right)^2=6^2\)
\(\Rightarrow\left[{}\begin{matrix}2x-1=6\\2x-1=-6\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2x=7\\2x=-5\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=-\dfrac{5}{2}\end{matrix}\right.\)
11 tháng 12 2021
a: Xét ΔABI và ΔACI có
AB=AC
AI chung
BI=CI
Do đó: ΔABI=ΔACI
27 tháng 10 2021
c: \(\dfrac{x}{5}=-\dfrac{3}{2}\)
nên \(x=-\dfrac{15}{2}\)