a.x^4=x^7
b.(2y+1)^6=(2y+1)^8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
a.
$x^2-2x-xy+2y=-3$
$(x^2-2x)-(xy-2y)=-3$
$x(x-2)-y(x-2)=-3$
$(x-2)(x-y)=-3$
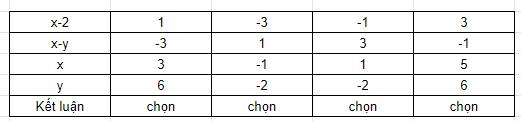
Vì $x,y$ nguyên nên $x-2, x-y$ nguyên. Ta có bảng sau:
b.
$xy-2y+x=-4$
$y(x-2)+(x-2)=-6$
$(x-2)(y+1)=-6$
Vì $x,y$ nguyên nên $x-2, y+1$ nguyên. Ta có bảng sau:

\(c.\left(x+1\right)\left(2y-1\right)=12\)
\(\Rightarrow\left(x+1\right)\left(2y-1\right)=4.3\)
\(\Rightarrow\orbr{\begin{cases}x+1=4\\2y-1=3\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=3\\y=2\end{cases}}\)

\(x^3-2x^2=x^2\left(x-2\right)\)
\(y^2+2y+1-x^2=\left(y+1\right)^2-x^2=\left(y+1-x\right)\left(y+1+x\right)\)
\(x^2-x-6=x^2+2x-3x-6=x\left(x+2\right)-3\left(x+2\right)=\left(x-3\right)\left(x+2\right)\)


a>x+y=5=> y=5-x
\(!x+1!+!3-x!\ge!x+1+3-x!=4\)
đẳng thức khi -1<=x<=3
=> xem lại đề

a: A=2/3x^2y+4x^2y=14/3x^2y
=14/3*9*7=294
b: B=xy^2(1/2+1/3+1/6)=xy^2=3/4*1/4=3/16
c: C=x^3y^3(2+10-20)=-8x^3y^3
=-8*1^3(-1)^3=8
d: D=xy^2(2018+16-2016)
=18xy^2
=18(-2)*1/9=-4
a). x^4 = x^7
=> x = \(\orbr{\begin{cases}0\\1\end{cases}}\)
b) (2y+1)^6 = (2y+1)^8
=> \(\orbr{\begin{cases}2y+1=0\\2y+1=1\end{cases}}\)
=> \(\orbr{\begin{cases}y=-\frac{1}{2}\\y=0\end{cases}}\)
`a,`
`x^4=x^7`
`->x^4-x^7=0`
`->x^4 (1 - x^3)=0`
TH1 : `x^4=0 ->x=0`
TH2 : `1-x^3=0 ->x^3=1^3 ->x=1`
Vậy `x=0,x=1`
`b,`
`(2y+1)^6 = (2y+1)^8`
`-> (2y+1)^6 - (2y+1)^8=0`
`-> (2y+1)^6 [1-(2y+1)^2]=0`
TH1 : `(2y+1)^6 =0 ->2y+1=0 ->y=(-1)/2`
TH2 : `1 - (2y+1)^2=0`
`-> (2y+1)^2=1`
`-> 2y+1=1` hoặc `2y+1=-1`
`->y=0` hoặc `y=-1`
Vậy `y=0,y=-1,y=(-1)/2`