
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số hoa của 3 bạn lần lượt là x, y , z
Vì x,y,z TLT vớ 4,5,6
=> x/4=y/5=z/6=k
Theo t/c dãy tỉ số bằng nhau :
k= x+y+z/ 4+5+6 = 75/15=5
=> x= 5.4=20
y= 5. 5 = 25
z= 5.6=30
Vậy ..
Gọi số hoa 3 bạn hái được lần lượt là a,b,c \(\left(a,b,c\inℕ^∗\right)\)
Theo đề bài ra,ta có :
\(\frac{a}{4}=\frac{b}{5}=\frac{c}{6}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ,ta có :
\(\frac{a}{4}=\frac{b}{5}=\frac{c}{6}=\frac{a+b+c}{4+5+6}=\frac{75}{15}=6\)
\(\Rightarrow\hept{\begin{cases}a=6.4=24\\b=6.5=30\\c=6.6=36\end{cases}}\)
Vậy ....

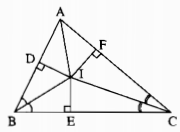
Kẻ: ID⊥AB,IE⊥BC,IF⊥ACID⊥AB,IE⊥BC,IF⊥AC
Xét hai tam giác vuông IDB và IEB, ta có:
\(\eqalign{
& \widehat {I{\rm{D}}B} = \widehat {IEB} = 90^\circ \cr
& \widehat {DBI} = \widehat {EBI}\left( {gt} \right) \cr} \)
BI cạnh huyền chung
⇒⇒ ∆IDB = ∆IEB (cạnh huyền, góc nhọn)
Suy ra: ID = IE (hai cạnh tương ứng)
Quảng cáo
Xét hai tam giác vuông IEC và IFC, ta có ;
\(\eqalign{
& \widehat {IEC} = \widehat {IFC} = 90^\circ \cr
& \widehat {ECI} = \widehat {FCI}\left( {gt} \right) \cr} \)
CI canh huyền chung
Suy ra: ∆ IEC = ∆IFC (cạnh huyền, góc nhọn)
Suy ra: IE = IF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông IDA và IFA, ta có:
ˆIDA=ˆIFA=90∘IDA^=IFA^=90∘
ID = IF (chứng minh trên)
AI cạnh huyền chung
Suy ra: ∆IDA = ∆IFA (cạnh huyền, cạnh góc vuông)
Suy ra: ˆDAI=ˆFAIDAI^=FAI^ (hai góc tương ứng)
Vậy AI là tia phân giác của ˆA
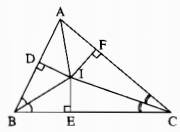
Kẻ: ID⊥AB,IE⊥BC,IF⊥ACID⊥AB,IE⊥BC,IF⊥AC
Xét hai tam giác vuông IDB và IEB, ta có:
ˆIDB=ˆIEB=90∘ˆDBI=ˆEBI(gt)IDB^=IEB^=90∘DBI^=EBI^(gt)
BI cạnh huyền chung
⇒⇒ ∆IDB = ∆IEB (cạnh huyền, góc nhọn)
Suy ra: ID = IE (hai cạnh tương ứng) (1)
Xét hai tam giác vuông IEC và IFC, ta có ;
ˆIEC=ˆIFC=90∘ˆECI=ˆFCI(gt)IEC^=IFC^=90∘ECI^=FCI^(gt)
CI canh huyền chung
Suy ra: ∆ IEC = ∆IFC (cạnh huyền, góc nhọn)
Suy ra: IE = IF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông IDA và IFA, ta có:
ˆIDA=ˆIFA=90∘IDA^=IFA^=90∘
ID = IF (chứng minh trên)
AI cạnh huyền chung
Suy ra: ∆IDA = ∆IFA (cạnh huyền, cạnh góc vuông)
Suy ra: ˆDAI=ˆFAIDAI^=FAI^ (hai góc tương ứng)
Vậy AI là tia phân giác của ˆA
Read more: https://sachbaitap.com/cau-100-trang-151-sach-bai-tap-sbt-toan-lop-7-tap-1-c7a10140.html#ixzz6DFwdbF2W


a)
$2HgO \xrightarrow{t^o} 2Hg + O_2$
n HgO = 21,6/217 = 0,1(mol)
n O2 = 1/2 n HgO = 0,05(mol)
V O2 = 0,05.22,4 = 1,12(lít)
b)
n HgO = 43,2/217 = 0,2(mol)
n O2 = 1/2 n HgO = 0,1(mol)
V O2 = 0,1.22,4 = 2,24(lít)
c)
n HgO = n Hg = 14,07/201 = 0,07(mol)
m HgO = 217.0,07 = 15,19(gam)




b) Tách các cặp tính trạng riêng ra :
P: AaBbDd x AaBBDd
-> (Aa x Aa) (Bb x BB) (Dd x Dd)
F1 : KG : (\(\dfrac{1}{4}\)AA : \(\dfrac{2}{4}\) Aa : \(\dfrac{1}{4}\) aa) ( \(\dfrac{1}{2}\) BB :\(\dfrac{1}{2}\) Bb) (\(\dfrac{1}{4}\)DD : \(\dfrac{2}{4}\) Dd : \(\dfrac{1}{4}\) dd )
KH : (\(\dfrac{3}{4}\)trội : \(\dfrac{1}{4}\) lặn) ( 100% trội ) (\(\dfrac{3}{4}\)trội : \(\dfrac{1}{4}\) lặn)
b1) Tỉ lệ biến dị tổ hợp ở đời con :
lặn, trội, lặn : \(\dfrac{1}{4}\) x 1 x \(\dfrac{1}{4}\) = \(\dfrac{1}{16}\)
lặn, trội, trội : \(\dfrac{1}{4}\) x 1 x \(\dfrac{3}{4}\) = \(\dfrac{3}{16}\)
b2)
Tỉ lệ 5 gen trội đời con :
AABBDd : \(\dfrac{1}{4}\) x \(\dfrac{1}{2}\) x \(\dfrac{2}{4}\) = \(\dfrac{1}{16}\)
AaBBDd : \(\dfrac{2}{4}\) x \(\dfrac{1}{2}\) x \(\dfrac{1}{4}\) = \(\dfrac{1}{16}\)





a/ A= { n|n là các số tự nhiên lớn hơn 12 và nhỏ hơn 30 }
b/ B= { n|n là số tự nhiên nhiên lớn hơn 21 và nhỏ hơn 43 }
c / C = { n|n là số tự nhiên lớn hơn 6 và nhỏ hơn 28 }
d/ D= {n|n là số tụ nhiên lớn hơn 3 và nhỏ hơn 50}