* Cho tam giác ABC vuông tại C. Biết cosA=\(\dfrac{5}{13}\). Tính tan B
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Ta có:
$\frac{5}{13}=\cos A=\frac{AC}{AB}$
$\Rightarrow AB=\frac{13}{5}AC$
Áp dụng định lý Pitago:
$AC^2+BC^2=AB^2$
$\Leftrightarrow AC^2+10^2=(\frac{13}{5}AC)^2$
$\Leftrightarrow 100=\frac{144}{25}AC^2$
$\Leftrightarrow AC^2=\frac{625}{36}$
$\Rightarrow AC=\frac{25}{6}$ (cm)
Vậy......

\(\overrightarrow{BA}=\left(3;0\right)\Rightarrow AB=3=AC\) ; \(\overrightarrow{AC}=\left(a-2;b+2\right)\) ; \(\overrightarrow{BC}=\left(a+1;b+2\right)\)
\(BC=\sqrt{AB^2+AC^2-2AB.AC.cosA}=\dfrac{6\sqrt{5}}{5}\)
\(\Rightarrow\left\{{}\begin{matrix}\left(a-2\right)^2+\left(b+2\right)^2=9\\\left(a+1\right)^2+\left(b+2\right)^2=\dfrac{36}{5}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(a;b\right)=\left(\dfrac{1}{5};-\dfrac{22}{5}\right)\\\left(a;b\right)=\left(\dfrac{1}{5};\dfrac{2}{5}\right)\end{matrix}\right.\)

Tam giác ABC vuông tại C
=> \(\sin B=\cos A=\frac{5}{15}\)
\(\sin^2B+\cos^2B=1\Rightarrow\cos B=\sqrt{1-\sin^2B}=\sqrt{1-\frac{5}{13}}=\sqrt{\frac{8}{13}}\)
\(\tan B=\frac{\sin B}{\cos B}=\frac{\frac{5}{13}}{\sqrt{\frac{8}{13}}}=\frac{\sqrt{26}}{12}\) \(\cot B=\frac{1}{\tan B}=\frac{12}{\sqrt{26}}\)

ta có:cosB=\(\dfrac{AB}{BC}=\dfrac{5}{13}\)⇒BC=39
AC=\(\sqrt{BC^2-AB^2}=\sqrt{39^2-15^2}\)=36

\(\sin^2\widehat{A}+\cos^2\widehat{A}=1\Leftrightarrow\cos^2\widehat{A}=1-\left(\dfrac{3}{5}\right)^2=1-\dfrac{9}{25}=\dfrac{16}{25}\\ \Leftrightarrow\cos\widehat{A}=\dfrac{4}{5}\\ \tan\widehat{A}=\dfrac{\sin\widehat{A}}{\cos\widehat{A}}=\dfrac{3}{4}\\ \Rightarrow\cot\widehat{A}=\dfrac{1}{\tan\widehat{A}}=\dfrac{4}{3}\)
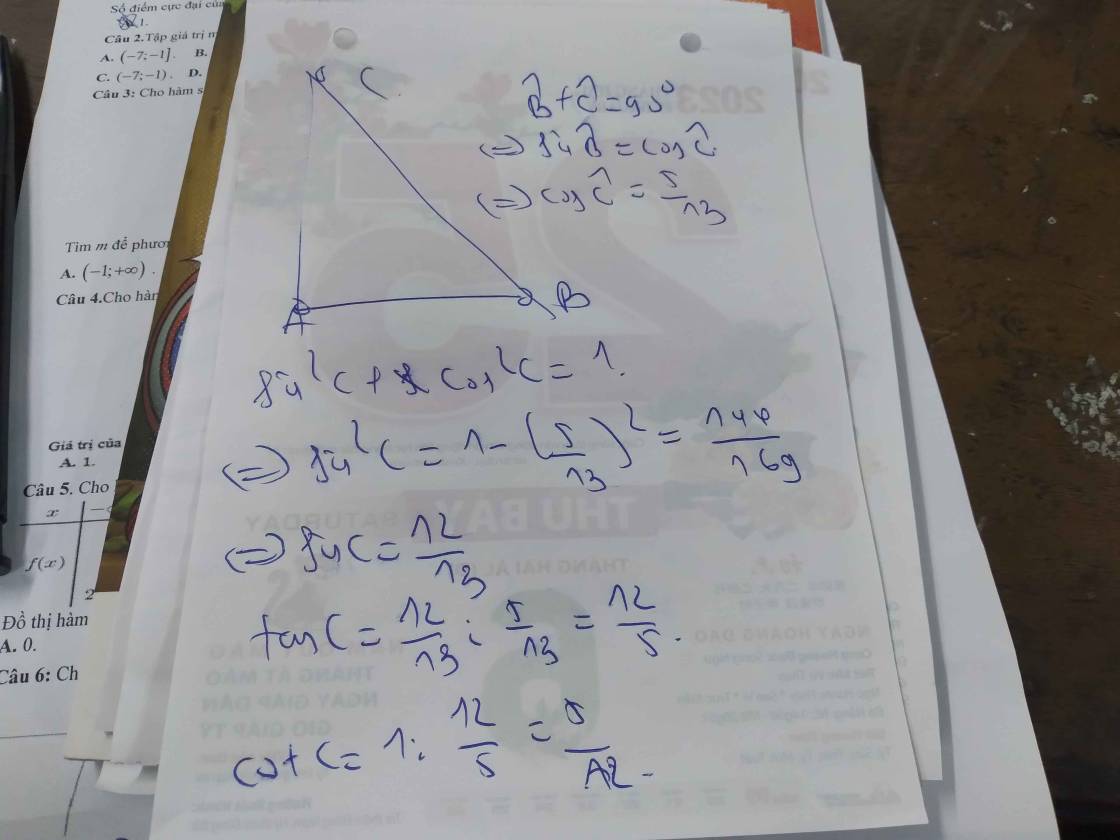
\(\sin\widehat{A}=\sqrt{1-\left(\dfrac{5}{13}\right)^2}=\dfrac{12}{13}\)
\(\cot\widehat{A}=\dfrac{5}{13}:\dfrac{12}{13}=\dfrac{5}{12}\)
\(\tan\widehat{B}=\dfrac{5}{12}\)