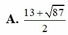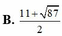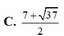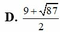Cho x, y, z, t thoả mãn điều kiện \(x^2+y^2+z^2+t^2=1\)và xy+yz+zt+tx=1. Tính giá trị của biểu thức \(A=\dfrac{2x-3y+4z}{5x-6y+7z}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 7 2017
a)
\(x^3+y^3+3\left(x^2+y^2\right)+4\left(x+y\right)+4=0\)
\(\Leftrightarrow\left(x^3+3x^2+3x+1\right)+\left(y^3+3y^2+3y+1\right)+\left(x+y+2\right)=0\)
\(\Leftrightarrow\left(x+1\right)^3+\left(y+1\right)^3+\left(x+y+2\right)=0\)
\(\Leftrightarrow\left(x+y+2\right)\left[\left(x+1\right)^2-\left(x+1\right)\left(y+1\right)+\left(y+1\right)^2\right]+\left(x+y+2\right)=0\)
\(\Leftrightarrow\left(x+y+2\right)\left[\left(x+1\right)^2-\left(x+1\right)\left(y+1\right)+\left(y+1\right)^2+1\right]=0\)
Lại có :\(\left(x+1\right)^2-\left(x+1\right)\left(y+1\right)+\left(y+1\right)^2+1=\left[\left(x+1\right)-\frac{1}{2}\left(y+1\right)\right]^2+\frac{3}{4}\left(y+1\right)^2+1>0\)
Nên \(x+y+2=0\Rightarrow x+y=-2\)
Ta có :
\(M=\frac{1}{x}+\frac{1}{y}=\frac{x+y}{xy}=\frac{-2}{xy}\)
Vì \(4xy\le\left(x+y\right)^2\Rightarrow4xy\le\left(-2\right)^2\Rightarrow4xy\le4\Rightarrow xy\le1\)
\(\Rightarrow\frac{1}{xy}\ge\frac{1}{1}\Rightarrow\frac{-2}{xy}\le-2\)
hay \(M\le-2\)
Dấu "=" xảy ra khi \(x=y=-1\)
Vậy \(Max_M=-2\)khi \(x=y=-1\)
12 tháng 7 2017
c) ( Mình nghĩ bài này cho x, y, z ko âm thì mới xảy ra dấu "=" để tìm Min chứ cho x ,y ,z dương thì ko biết nữa ^_^ , mình làm bài này với điều kiện x ,y ,z ko âm nhé )
Ta có :
\(\hept{\begin{cases}2x+y+3z=6\\3x+4y-3z=4\end{cases}\Rightarrow2x+y+3z+3x+4y-3z=6+4}\)
\(\Rightarrow5x+5y=10\Rightarrow x+y=2\)
\(\Rightarrow y=2-x\)
Vì \(y=2-x\)nên \(2x+y+3z=6\Leftrightarrow2x+2-x+3z=6\)
\(\Leftrightarrow x+3z=4\Leftrightarrow3z=4-x\)
\(\Leftrightarrow z=\frac{4-x}{3}\)
Thay \(y=2-x\)và \(z=\frac{4-x}{3}\)vào \(P\)ta có :
\(P=2x+3y-4z=2x+3\left(2-x\right)-4.\frac{4-x}{3}\)
\(\Rightarrow P=2x+6-3x-\frac{16}{3}+\frac{4x}{3}\)
\(\Rightarrow P=\frac{x}{3}+\frac{2}{3}\ge\frac{2}{3}\)( Vì \(x\ge0\))
Dấu "=" xảy ra khi \(x=0\Rightarrow\hept{\begin{cases}y=2\\z=\frac{4}{3}\end{cases}}\)( Thỏa mãn điều kiện y , z ko âm )
Vậy \(Min_P=\frac{2}{3}\)khi \(\hept{\begin{cases}x=0\\y=2\\z=\frac{4}{3}\end{cases}}\)
PT
2
S
6 tháng 7 2018
Ta có: \(x^2+y^2+z^2+t^2-\left(xy+yz+zt+tx\right)=1-1\)
\(\Leftrightarrow2\left(x^2+y^2+z^2+t^2-xy-yz-zt-tx\right)=0\)
\(\Leftrightarrow2x^2+2y^2+2z^2+2t^2-2xy-2yz-2zt-tx=0\)
\(\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(y^2-2yz+z^2\right)+\left(z^2-2zt+t^2\right)+\left(t^2-2tx+x^2\right)=0\)
\(\Leftrightarrow\left(x-y\right)^2+\left(y-z\right)^2+\left(z-t\right)^2+\left(t-x\right)^2=0\)
Vì \(\left(x-y\right)^2\ge0;\left(y-z\right)^2\ge0;\left(z-t\right)^2\ge0;\left(t-x\right)^2\ge0\)
\(\Rightarrow\left(x-y\right)^2+\left(y-z\right)^2+\left(z-t\right)^2+\left(t-x\right)^2\ge0\)
Dấu "=" xảy ra khi x - y = 0 ; y - z = 0 ; z - t = 0 ; t - x = 0 <=> x = y = z = t
Khi đó \(x^2+y^2+z^2+t^2=x^2+x^2+x^2+x^2=4x^2=1\)
\(\Leftrightarrow x^2=\frac{1}{4}\Leftrightarrow x=\pm\frac{1}{2}\)
Vậy \(x=y=z=t=\pm\frac{1}{2}\)
9 tháng 9 2018
a) đề bị thiếu nha
ta có : \(x^2+y^2+z^2+t^2=1\) và \(xy+yz+zt+tx=1\)
\(\Leftrightarrow2x^2+2y^2+2z^2+2t^2-2xy-2yz-2zt-2tx=0\)
\(\Leftrightarrow\left(x-y\right)^2+\left(y-z\right)^2+\left(z-t\right)^2+\left(t-x\right)^2=0\)
\(\Leftrightarrow x=y=z=t\)
\(\Rightarrow x^2+y^2+z^2+t^2=1\Leftrightarrow4x^2=1\Leftrightarrow x=\pm\dfrac{1}{2}\)
\(\Rightarrow x=y=z=t=\pm\dfrac{1}{2}\)
b) ta có : \(x+y+z=6\) và \(x^2+y^2+z^2=12\)
\(\Rightarrow x^2+y^2+z^2-4x-4y-4z+12=0\)
\(\Leftrightarrow\left(x-2\right)^2+\left(y-2\right)^2+\left(z-2\right)^2\Leftrightarrow x=y=z=2\)