Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Vì đa thức 13 x 4 y 3 - 5 x 3 y 3 + 6 x 2 y 2 chia hết cho 5 x n y n nên mỗi hạng tử của đa thức trên chia hết cho 5 x n y n Do đó, hạng tử 6 x 2 y 2 chia hết cho 5 x n y n ⇒ 0 ≤ n ≤ 2 . Vậy n ∈ {0;1;2}
Vì đa thức 5 x 3 - 7 x 2 + x chia hết cho 3 x n nên mỗi hạng tử của đa thức chia hết cho x n
=> hạng tử x – có số mũ nhỏ nhất của đa thức chia hết cho 3 x n
Do đó, x : x n ⇒ 0 ≤ x ≤ 1 . Vậy n ∈ {0; 1}
x n y n + 1 : x 2 y 5 = x n : x 2 y n + 1 : y 5 = x n - 2 . y n - 4 là phép chia hết
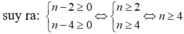
x 4 : x n = x 4 - n là phép chia hết nên 4 – n ≥ 0 ⇒ 0 ≤ n ≤ 4
suy ra: n ∈ {0; 1; 2; 3; 4}
5 x n y 3 : 4 x 2 y 2 = 5/4 x n : x 2 y 3 : y 2 = 5/4 x n - 2 . y là phép chia hết
Suy ra: n – 2 ≥ 0 ⇒ n ≥ 2
Bài 1:
a) 35.43 + 35.56 + 35
= 35. (43 + 56 + 1)
= 35. (99 + 1)
= 35.100
= 3500
b) 40 + (139 – 172 + 99) – (139 + 199 – 172)
= 40 + 139 – 172 + 99 – 139 – 199 + 172
= 40 + (139 – 139) + (172 – 172) + (99 – 199)
= 40 + 0 + 0 + (-100)
= -60
Bài 5:
Theo đề bài, ta có :
n + 6 chia hết cho n , n cũng chia hết cho n
Mặt khác :
[(n + 6) - n] chia hết cho n \(\leftrightarrow\) (n + 6 - n) chia heet cho n
Vậy N là ước của 6 nên:
\(Ư\left(6\right)=\left\{\pm1;\pm2;\pm3;\pm6\right\}\)
N là số nguyên dương : \(n\in\left\{1;2;3;6\right\}\)
Vậy......
5:
n+6 chia hết cho n
=>6 chia hết cho n
mà n là số tự nhiên
nên n thuộc {1;2;3;6}
1:
a: =35(43+56+1)=35*100=3500
b: =40+139+99-172-139-199+172
=40-40=0
\(x^ny^{n+1}:x^2y^5=x^{n-2}.y^{n-4}\)
Để \(x^ny^{n+1}⋮x^2y^5\) thì \(\hept{\begin{cases}n-2\ge0\\n-4\ge0\end{cases}\Leftrightarrow}\hept{\begin{cases}n\ge2\\n\ge4\end{cases}}\Leftrightarrow n\ge4.\)
1. Tìm n để mỗi phép chia sau là phép chia hết (\(n\) là số tự nhiên)
a. Vì đa thức \((5x^3-7x^2+x)\) chia hết cho \(3x^n\) nên mỗi hạng tử của đa thức chia hết cho \(xn\)
=> hạng tử \(x\) – có số mũ nhỏ nhất của đa thức chia hết cho \(3x^n\) .
Do đó, \(x:xn\) \(\Rightarrow0\le n\le1\). Vậy \(n\in\text{{}0;1\)
b. Vì đa thức \((13x^4y^3-5x^3y^3+6x^2y^2)\) chia hết cho \(5x^ny^n\) nên mỗi hạng tử của đa thức trên chia hết cho \(5x^ny^n\) Do đó, hạng tử \(6x^2y^2\)chia hết cho \(5x^ny^n\) \(\Rightarrow0\le n\le2\) . Vậy \(n\in\text{ {}0;1;2\)
2 Thực hiện phép tính:
\(a.(7.3^5-3^4+3^6):3^4\)
\(=(7.3^5:3^4)+(3^6:3^4)\)
\(=7.3-1+3^2\)
\(=21-1+9=29\)
\(b.(16^3-64^2):8^3\)
\(=(16^3:8^3)-(64^2:8^3)\)
\(=(16:8)^3-(8^4:8^3)(\)vì \(64=8^2\)nên \(64^2=(8^2)^2=8^4)\)
\(=2^3-8=8-8=0\)