Ba đường thẳng aa' ,bb' ,cc' cùng đi qua điểm O. Hãy kể tên các đỉnh nhỏ hơn góc bẹt
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1. Em hãy chọn trong các phương án dưới đây để được một phát biểu đúng.
Qua hai điểm A và B phân biệt có
(A) vô số đường thẳng (B) Chỉ có 1 đường thẳng
(C) không có đường thẳng nào
![]()
Đáp án: B
Bài 2. Vẽ hình cho các trường hợp sau:
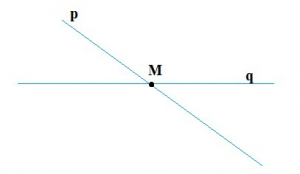
a) Hai đường thẳng p và q cắt nhau tại điểm M
b) Đường thẳng a cắt hai đường thẳng m và n theo thứ tự tại X và Y trong hai trường hợp m và n cắt nhau, hoặc m và n song song với nhau
![]()
a)


Ba đường thẳng aa' , bb' , cc' tạo thành 6 góc: \(\widehat{aOb};\widehat{bOc};\widehat{cOa'};\widehat{a'Ob'};\widehat{b'Oc'};\widehat{c'Oa}\) có tổng bằng 360 độ
G/S: Trong các góc này không có góc nào nhỏ hơn hoặc bằng 60 độ
=> Cả 6 góc đều lớn hơn 60 độ
=> Tổng 6 góc > 60.6=360 độ vô lí
=> Phải có ít nhất một góc nhỏ hơn hoặc bằng 60 độ

tuổi con HN là :
50 : ( 1 + 4 ) = 10 ( tuổi )
tuổi bố HN là :
50 - 10 = 40 ( tuổi )
hiệu của hai bố con ko thay đổi nên hiệu vẫn là 30 tuổi
ta có sơ đồ : bố : |----|----|----|
con : |----| hiệu 30 tuổi
tuổi con khi đó là :
30 : ( 3 - 1 ) = 15 ( tuổi )
số năm mà bố gấp 3 tuổi con là :
15 - 10 = 5 ( năm )
ĐS : 5 năm
mình nha
2 cặp góc đối đỉnh là \(\widehat{xOy}\)và \(\widehat{tOz}\)
\(\widehat{xot}\)và \(\widehat{yOz}\)
Ta có:
\(\widehat{xOy}=\widehat{zOt}=100^0\)(đối đỉnh)
\(\widehat{yOx}+\widehat{xOt}=180^0\)(2 góc kề bù)
\(100^0+\widehat{xOt}=180^0\)
\(\widehat{xOt}=80^0\)
=>\(\widehat{yOz}=80^0\left(=\widehat{xOt}\right)\)
Vậy \(\widehat{zOt}=100^0;\widehat{xOt}=\widehat{yOz}=80^0\)

mình làm cách này nhé:
gọi O, I là giao 2 đường chéo của hv ABCD và A'B'C'D'
ta có :
PO//=MI
QO//=IN
suy ra tam giác POQ= tam giác MIN (c-g-c)
tương tự PON=MIQ(c-g-c)
từ đó lấy góc và cạnh sẽ được