Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
b1 :
DE // AB
=> góc ABC = góc DEC (đồng vị)
góc ABC = góc ACB do tam giác ABC cân tại A (gt)
=> góc DEC = góc ACB
=> tam giác DEC cân tại D (dh)
b2:
a, tam giác ABC => góc A + góc B + góc C = 180 (đl)
góc A = 80; góc B = 50
=> góc C = 50
=> góc B = góc C
=> tam giác ABC cân tại A (dh)
b, DE // BC
=> góc EDA = góc ABC (slt)
góc DEA = góc ECB (dlt)
góc ABC = góc ACB (Câu a)
=> góc EDA = góc DEA
=> tam giác DEA cân tại A (dh)
Bài 1:
Tam giác MNP có: \(\widehat{M}=40^o;\widehat{N}=100^o\)
Tổng số đo 3 góc của 1 tam giác là 180o, ta được:
\(\widehat{M}+\widehat{N}+\widehat{P}=180^o\\ \Leftrightarrow40^o+100^o+\widehat{P}=180^o\\ \Leftrightarrow140^o+\widehat{P}=180^o\\ \Leftrightarrow\widehat{P}=180^o-140^o=40^o\)
Vì: \(\widehat{M}=\widehat{P}=40^o\) => Tam giác MNP là tam giác cân tại N (ĐPCM)
a: Xét ΔADE có
AG vừa là đường cao, vừa là phân giác
nên ΔADE cân tại A
=>AD=AE
b: góc BFD=góc DEA
góc BDF=góc BEA
Do đo: góc BFD=góc BDF
=>ΔBFD cân tại B
c: Xét ΔBMF và ΔCME có
góc BMF=góc CME
MB=MC
góc MBF=góc MCE
Do đó: ΔBMF=ΔCME
=>BF=CE=BD
a: Xét ΔADE có
AG vừa là đường cao, vừa là phân giác
nên ΔADE cân tại A
=>AD=AE
b: góc BFD=góc DEA
góc BDF=góc BEA
Do đo: góc BFD=góc BDF
=>ΔBFD cân tại B
c: Xét ΔBMF và ΔCME có
góc BMF=góc CME
MB=MC
góc MBF=góc MCE
Do đó: ΔBMF=ΔCME
=>BF=CE=BD
Mk thấy đề sai hay sao ý ko có đường thẳng nào đi qua B song song vs CD và cắt DM cả
mik thấy cô ghi đè s mik ghi lại y chang chứ mik ko bik j cả. mik đọc cx thấy sai sai cái j á mà ko bik mik đọc đè đúng hay là sai nên mik mới đăng
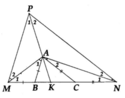
\(\Delta ABC\) cân có \(\widehat{ABC}=60^0\)
\(\Rightarrow\Delta ABC\) là tam giác đều
Xét \(\Delta MNC\) có :
Vì \(\Delta ABC\) là tam giác đều
\(\Rightarrow\widehat{BAC}=\widehat{ABC}=\widehat{ACB}=60^0\)
Vì AB // MN
\(\Rightarrow\widehat{BAC}=\widehat{NMC}=60^0\) (đồng vị)
Vì AB // MN
\(\Rightarrow\widehat{ABC}=\widehat{MNC}=60^0\)(đồng vị)
\(\Rightarrow\Delta MNC\) cân tại C
Mà \(\widehat{ACB}=60^0\)
\(\Rightarrow\Delta CMN\) là tam giác đều
b Xét \(\Delta MKC\) và \(\Delta NKC\) có :
MC = NC (Vì \(\Delta CMN\) là tam giác đều)
Vì \(\widehat{AHC}=90^0\)
\(\Rightarrow\widehat{HAC}+\widehat{ACH}=90^0\)
\(\Rightarrow60^0+\widehat{ACH}=90^0\)
\(\Rightarrow\widehat{ACH}=30^0\)
\(\Rightarrow\dfrac{\widehat{ACB}}{2}=\widehat{ACH}\)
\(\Rightarrow CH\) là tia phân giác của \(\widehat{ACB}\)
\(\Rightarrow\widehat{ACH}=\widehat{BCH}\)
KC : cạnh chung
\(\Rightarrow\Delta MKC=\Delta NKC\) (c . g . c)
\(\Rightarrow\widehat{MKC}=\widehat{CKN}\)
Mà \(\widehat{MKC}+\widehat{NKC}=180^0\)
\(\Rightarrow\widehat{MKC}=\widehat{NKC}=\dfrac{1}{2}\times180^0=90^0\)
\(\Rightarrow CK\perp MN\)
Vì \(\Delta MKC=\Delta NKC\)
\(\Rightarrow MK=NK\)
\(\Rightarrow MK=\dfrac{1}{2}\times MN\)
Mà MN = CM
\(\Rightarrow MK=\dfrac{1}{2}\times MC\)