Cho tram giác ABC vuông tại A.Kẻ AH vuông góc với BC.Chứng minh rằng:
a) AC2 = CH . BC
b)AH2 = BH . CH
Sử dụng định lý Pitago nhé!Làm ơn giúp vs ạ!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 1 2018
Có t/g BAC đồng dạng với AHC ( góc góc )
suy ra \(\frac{BC}{AC}=\frac{AC}{HC}\)
Nhân chéo nó lên tao được
\(BC.HC=AC.AC\Leftrightarrow BC.HC=AC^2\) (1)
xét tiếp tam giác BHA đồng dạng với AHC ( góc góc )
suy ra \(\frac{BH}{AH}=\frac{HA}{HC}\) Lại nhân chéo nó lên tao được
\(BH.HC=AH.HA\Leftrightarrow BH.CH=AH^2\) (2)
từ 1 và 2 suy ra được Pain luôn đúng , làm ny anh nhé baby
8 tháng 2 2021
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+HB^2\)
Áp dụng định lí Pytago vào ΔACH vuông tại H, ta được:
\(AC^2=CH^2+AH^2\)
hay \(CH^2=AC^2-AH^2\)
Ta có: \(AB^2+CH^2=AH^2+BH^2+AC^2-AH^2\)
nên \(AB^2+CH^2=AC^2+BH^2\)(đpcm)
CM
2 tháng 10 2017
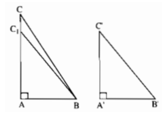
Do AC > A'C' nên lấy được điểm C1 trên cạnh AC sao cho AC1=A′C′. Ta có tam giác vuông ABC1 bằng tam giác vuông A'B'C', suy ra B′C′=BC1. Mặt khác hai đường xiên BC và BC1 kẻ từ B đến đường thẳng AC lần lượt có hình chiếu trên AC là AC và AC1. Vì AC > AC1 nên BC > BC1. Suy ra BC > B'C'.
13 tháng 5 2023
b: BE>BC+CE
=BC+1/2CH
=BC+1/2*1/2(HB+HC)
=BC+1/4(HB+HC)>BC+1/4BC
=>BE>5/4BC>3/BC
1 tháng 11 2023
c: Xét ΔAHB vuông tại H có \(AE\cdot AB=AH^2\)
=>\(AE=\dfrac{AH^2}{AB}\)
Xét ΔAHC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\)
=>\(AF=\dfrac{AH^2}{AC}\)
XétΔABC vuông tại A có
\(tanC=\dfrac{AB}{AC}\)
\(\dfrac{AF}{AE}=\dfrac{AH^2}{AC}:\dfrac{AH^2}{AB}=\dfrac{AB}{AC}=tanC\)
=>\(AF=AE\cdot tanC\)
18 tháng 5 2022
a: Do AC > A'C' nên lấy được điểm C1 trên cạnh AC sao cho AC1=A′C′.
Ta có ΔABC1=ΔA'B'C'
Suy ra B′C′=BC1
Mặt khác hai đường xiên BC và BC1 kẻ từ B đến đường thẳng AC lần lượt có hình chiếu trên AC là AC và AC1.
Vì AC > AC1 nên BC > BC1.
Suy ra BC > B'C'.
b:
-Giả sử AC<A'C'.
Khi đó theo chứng minh câu a) ta có BC < B'C'. Điều này không đúng với giả thiết BC > B'C'.
Giả sử AC=A'C'. Khi đó ta có ΔABC=ΔA'B'C' (c.g.c).
Suy ra BC=B'C'.
Điều này cũng không đúng với giả thiết BC>B'C'. Vậy ta phải có AC>A'C'.
23 tháng 7 2023
a) \(AH^2=BH.CH=3,6.6,4=23,04\)
\(\Rightarrow AH=4,8\left(cm\right)\)
\(AC^2=AH^2+HC^2=23,04+40,96=64\)
\(\Rightarrow AC=8\left(cm\right)\)
\(AB^2=AH^2+BH^2=23,04+12,96=36\)
\(\Rightarrow AB=6\left(cm\right)\)
\(BC=BH+CH=3,6+6,4=10\left(cm\right)\)
\(tanB=\dfrac{8}{6}=\dfrac{4}{3}\Rightarrow B=53^o\)
\(\Rightarrow C=90^o-53^o=37^o\)
b) Xét Δ vuông ABH, có đường cao DH ta có :
\(AH^2=AD.AB\left(1\right)\)
Tương tự Δ vuông ACH :
\(AH^2=AE.AC\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow AD.AB=AE.AC\)
a: Xét ΔABC vuông tại A có AH là đường cao
nên \(AC^2=CH\cdot CB\)(hệ thức lượng)
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(HA^2=HB\cdot HC\)(hệ thức lượng)