Một xe cát có khối lượng 50kg đang chuyển động với vận tốc 10m/s trên mặt phẳng ngang. Người ta bắn một viên đạn có khối lượng 10g vào với vận tốc 200m/s hợp với phương ngang góc 600. Viên đạn cắm vào...

NT

Nguyễn Thùy Trang

17 tháng 1 2018

Một xe cát có khối lượng 50kg đang chuyển động với vận tốc 10m/s trên mặt phẳng ngang. Người ta bắn một viên đạn có khối lượng 10g vào với vận tốc 200m/s hợp với phương ngang góc 600. Viên đạn cắm vào cát và xe tiếp tục chuyển động. Thời gian va chạm là 0.15s. Tính vận tốc của xe cát sau va chạm a. Viên đạn bay cùng chiều chuyển động của xe . b. Viên đạn bay ngược chiều chuyển động của...

Đọc tiếp

#Vật lý lớp 10

0

HD

Hoàng Đức Long

3 tháng 1 2017

Một viên đạn đang bay theo phương ngang với vận tốc 600 m/s thì xuyên vào một xe cát nhỏ, khối lượng M = 1,5 kg đang chuyển động ngược hướng trên mặt ngang với vận tốc 0,5 m/s và ngay sau đó đạn nằm yên trong xe. Bỏ qua ma sát giữa xe và mặt đường. Tốc độ của xe sau khi đạn đã nằm yên trong cát là 7,4 m/s theo hướng chuyển động ban đầu của viên đạn. Khối lượng của viên đạn là:...

Đọc tiếp

#Vật lý lớp 10

1

VT

Vũ Thành Nam

3 tháng 1 2017

Lời giải

Sau va chạm 2 vật dính vào nhau và cùng chuyển động với cùng một vận tốc => 2 vật va chạm mềm.

Chọn chiều dương là chiều chuyển động của viên đạn

Gọi v 1 , v 2 , V lần lượt là vận tốc viên đạn, xe lúc trước là xe lúc sau va chạm. Ta có:

m 1 v 1 + m 2 v 2 = m 1 + m 2 V ⇒ V = m 1 v 1 + m 2 v 2 m 1 + m 2 ⇔ 7 , 4 = m 1 .600 − 1 , 5.0 , 5 m 1 + 1 , 5 ⇔ m 1 = 0 , 02 k g = 20 g

Với v 2 = − 0 , 5 m / s vì xe chuyển động ngược chiều so với viên đạn

Đáp án: A

Đúng(0)

HD

Hoàng Đức Long

5 tháng 3 2018

Bắn một viên đạn khối lượng m = 10g với vận tốc v vào một mẩu gỗ khối lượng M = 390g đặt trên mặt bàn ngang nhẵn. Đạn mắc vào gỗ và cùng chuyển động với vận tốc v12 = 10m/s. Lượng động năng của đạn đã chuyển thành nhiệt là A. 780J B. 650J C. 580J D....

Đọc tiếp

#Vật lý lớp 10

1

VT

Vũ Thành Nam

5 tháng 3 2018

Đáp án A

Xét tại vị trí va chạm thế năng không đổi nên sự biến thiên cơ năng chính là sự biến thiên động năng nó chuyển thành nhiệt tỏa ra khi va chạm

- Áp dụng định luật bảo toàn động lượng của hệ.

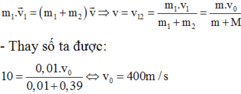
- Ta có công thức giải nhanh trong quá trình va chạm mềm cơ năng của hệ bị giảm. Phần cơ năng giảm này đã chuyển hóa thành nhiệt năng. Nói cách khác ta có công thức nhiệt tỏa ra trong va chạm:

Đúng(0)

VT

Vũ Thị Hồng Nhung

6 tháng 5 2021

Người ta bắn một viên đạn khối lượng 10g và vận tốc 500m/s vào bao cát khối lượng 12 kg theo phương thẳng đứng nhờ một sợi dây dài. sau khi viên đạn cắm vào bao cát cả hai cùng chuyển động với vận tốc bao nhiêu?

#Vật lý lớp 10

0

VN

Vicky Nguyễn

23 tháng 2 2020

Một xe cát có khối lượng kg đang chuyển động vs vận tốc m/s trên mặt phẳng ngang. Người ta bắn một viên đạn khối lượng 10g vào với vận tốc 200m/s hợp vs phương ngang góc 60. Viên đạn cắm vào cát và xe tiếp tục chuyển động.Thời gian va chạm là 0,15s.Tính vận tốc của xe cát sau va chạm. a) Viên đạn bay cừng chiều chuyển động của xe. b) Viên đạn bay ngược chiều chuyển động của...

Đọc tiếp

#Vật lý lớp 10

0

HD

Hoàng Đức Long

10 tháng 2 2017

Một viên đạn pháo khối lượng m1 = 10 kg bay ngang với vận tốc v1 = 500 m/s dọc theo đường sắt và cắm vào toa xe chở cát có khối lượng m2 = 1 tấn, đang chuyển động cùng chiều với vận tốc v2 = 36 km/h. Vận tốc của toa xe ngay sau khi trúng đạn là A. 4,95 m/s B. 15 m/s C. 14,85 m/s D. 4,5...

Đọc tiếp

#Vật lý lớp 10

1

VT

Vũ Thành Nam

10 tháng 2 2017

Đúng(0)

HD

Hoàng Đức Long

3 tháng 6 2019

Một khẩu pháo có khối lượng m1 = 130kg được đặt trên một toa xe nằm trên đường ray biết to axe có khối lượng m2 = 20kg khi chưa nạp đạn. Viên đạn được bắn ra theo phương nằm ngang dọc theo đường ray biết viên đạn có khối lượng m3 = 1kg. Vận tốc của đạn khi bắn ra khỏi nòng súng thì có vận tốc v0 = 400m/s so với súng. Hãy xác định vận tốc của toa xe sau khi bắn trong các trường...

Đọc tiếp

#Vật lý lớp 10

1

VT

Vũ Thành Nam

3 tháng 6 2019

Chiều (+) là chiều CĐ của đạn:

a. Toa xe đứng yên v = 0 p = 0

Theo định luật bảo toàn động lượng ta có:

( m 1 + m 2 + m 3 ) v = ( m 1 + m 2 ) v / + m 3 v 0 ⇒ v / = ( m 1 + m 2 + m 3 ) v − m 3 . v 0 m 1 + m 2 = 0 − 1.400 130 + 20 ≈ − 2 , 67 m / s

Toa xe CĐ ngược chiều với chiều viên đạn

b. Theo định luật bảo toàn động lượng ta có:

( m 1 + m 2 + m 3 ) v 1 = ( m 1 + m 2 ) v / + m 3 ( v 0 + v 1 ) ⇒ v / = ( m 1 + m 2 + m 3 ) v 1 − m 3 . ( v 0 + v 1 ) m 1 + m 2 ⇒ v / = ( 130 + 20 + 1 ) .5 − 1. ( 400 + 5 ) 130 + 20 ≈ 2 , 33 ( m / s )

Toa xe CĐ theo chiều bắn nhưng vận tốc giảm đi.

c. Theo định luật bảo toàn động lượng ta có

− ( m 1 + m 2 + m 3 ) v 1 = ( m 1 + m 2 ) v / + m 3 ( v 0 − v 1 ) ⇒ v / = − ( m 1 + m 2 + m 3 ) v 1 − m 3 . ( v 0 − v 1 ) m 1 + m 2 ⇒ v / = − ( 130 + 20 + 1 ) .5 − 1. ( 400 − 5 ) 130 + 20 ≈ − 7 , 67 ( m / s )

Vận tốc của toa vẫn theo chiều cũ và tăng tốc.

Đúng(0)

HD

Hoàng Đức Long

10 tháng 11 2018

Viên đạn khối lượng m = 10g đang bay đến với vận tốc v = 100 m/s cắm vào bao cát khối lượng M = 490g treo trên dây dài ℓ = 1m và đứng yên. Sau khi đạn cắm vào, bao cát chuyển động với vận tốc bao nhiêu?

A. 2m/s

B. 0,2m/s

C. 5m/s

D. 0,5m/s

#Vật lý lớp 10

1

VT

Vũ Thành Nam

10 tháng 11 2018

Đúng(0)

HD

Hoàng Đức Long

21 tháng 6 2017

Viên đạn khối lượng m=10g đang bay đến với vận tốc v=100m/s cắm vào bao cát khối lượng M=490g treo trên dây dài l=1m và đứng yên

Sau khi đạn cắm vào, bao cát chuyển động với vận tốc bao nhiêu?

A. 2m/s

B. 0,2m/s

C. 5m/s

D. 0,5m/s

#Vật lý lớp 10

1

VT

Vũ Thành Nam

21 tháng 6 2017

Đáp án A

V = m m + M v = 2 m / s

Đúng(0)

SB

Sonyeondan Bangtan

23 tháng 2 2021

Để đo vận tốc của viên đạn người ta treo một bao cát có khối lượng M=2,8kg vào một sợi dây nhẹ không giãn. Viên đạn có khối lượng m=16g được bắn theo phương ngang và găm vào bao cát, đẩy bao cát lên một độ cao h=0,8m. Lấy g=10m/s^2 a) Tính vận tốc của bao cát ngay sau khi viên đạn găm vàob) Tính vận tốc của viên đạn trước khi xuyên vào bao...

Đọc tiếp

#Vật lý lớp 10

1

HQ

Hồng Quang

23 tháng 2 2021

chọn mốc thế năng tại điểm thấp nhất ( trùng với phương bay của đạn )

Vật chỉ chịu tác dụng của trọng lực cơ năng được bảo toàn: ( Bảo toàn cho hệ lúc vừa cắm vào bao cát đến lúc bao cát lên 1 đoạn h=0,8(m) )

a) \(W_1=W_2\Leftrightarrow\dfrac{1}{2}\left(m+M\right)v_1^2=\left(m+M\right)gz_2\) \(\Rightarrow v_1=\sqrt{\dfrac{2\left(m+M\right)gz_2}{m+M}}=4\left(m/s\right)\)

b) Bảo toàn động lượng:

\(mv_0=\left(m+M\right)v_1\Rightarrow v_0=\dfrac{\left(m+M\right)v_1}{m}=704\left(m/s\right)\)

Đúng(2)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP