Bài 1: Cho tam giác AOB có OA = OB. Tia phân giác của góc O cắt AB ở D. Chứng minh rằng:
a. DA = DB
b. OD ⊥AB
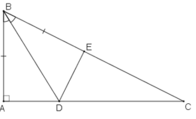
Bài 2: Cho tam giác ABC có ∠A =90o, trên cạnh BC lấy điểm E sao cho BE = BA. Trên tia phân giác của góc B cắt AC ở D
a, So sánh các độ dài DA và DE
b, Tính số đo góc BED
Giúp mk vs mn ơi, mk phải làm bài tập cô giao!

Bài 1:
a, Xét ΔAOD và ΔBOD, ta có:
OA = OB (gt)
∠(AOD) = ∠(BOD)(vì OD là tia phân giác)
OD cạnh chung
Suy ra: ΔAOD= ΔBOD(c.g.c)
Vậy: DA = DB (hai cạnh tương ứng)
b, ΔAOD= ΔBOD (chứng minh trên)
⇒ ∠(ADO) = ∠(BDO) (hai góc tương ứng) (1)
Ta có: ∠(ADO) + ∠(BDO) =180o(hai góc kề bù) (2)
Từ (1) và (2) suy ra: ∠(ADO) = ∠(BDO) =90o
Vậy: OD ⊥AB
Bài 2:
a, Xét ΔABD và ΔEBD, ta có:
AB = BE (gt)
∠(ABD) = ∠(DBE) (vì BD là tia phân giác)
BC cạnh chung
Suy ra: ΔABD = ΔEBD(c.g.c)
⇒ DA = DE (hai cạnh tương ứng)
b, Ta có: ΔABD = ΔEBD(chứng minh trên)
Suy ra: ∠A = ∠(BED) (hai góc tương ứng)
Mà ∠A =90onên ∠(BED) =90o