Người ta muốn mạ vàng cho một cái hộp có đáy hình vuông, không nắp, thể tích hộp là 4 lít Giả sử độ dày lớp mạ tại mọi điểm trên một là như nhau.Gọi chiều cao và cạnh đáy hộp lần lượt là h và x. Giá trị của x và h để lượng vàng cần dùng nhỏ nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

23 tháng 2 2017
2, thể tích cái hộp đó là:
59 x 46 x 17 = 46138(cm)
Nếu sai nhớ bảo mình nhé còn đúng thì k và kết bạn vs mình

CM
15 tháng 1 2017
Gọi chiều rộng của nắp hộp là x và giá thành 1 đơn vị diện tích làm nắp hộp là a (cố định).
Khi đó giá thành làm 1 đơn vị diện tích mặt bên là 3a.
Chiều dài nắp hộp là 2x nên thể tích hình hộp chữ nhật là

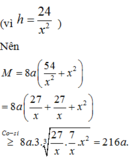
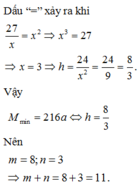
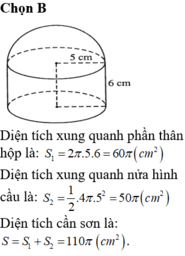
Chọn C.


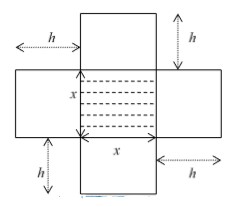
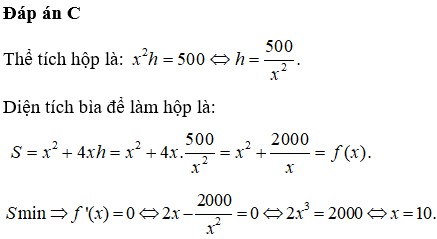
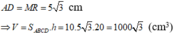
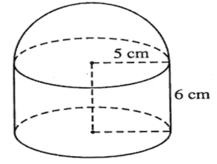
Gọi cạnh đáy là \(a\) , chiều cao là \(h\)
Diện tích đáy là: \(a2\).
Diện tích xung quanh là: \(4ah\)
Ta có:\(V=a^2.h=4\Rightarrow ah=\dfrac{4}{a}\left(\cdot\right)\)
Lượng vàng cần phải dùng là: \(a^2+4ah=a^2+\dfrac{16}{a}\)
Xét hàm số \(f\left(a\right)=a^2+\dfrac{16}{a};a>0\)
Ta có: \(f'\left(a\right)=2a-\dfrac{16}{a^2}\)
\(f'\left(a\right)=0\Leftrightarrow2a-\dfrac{16}{a^2}=0\Leftrightarrow\dfrac{2a^3-16}{a}=0\Leftrightarrow a=2\)
Lập bảng biến thiên ta thấy hàm số \(f\left(a\right)\) đạt giá trị nhỏ nhất tại \(a=2\), thay vào \(\left(\cdot\right)\) suy ra \(h=1\)
Gọi cạnh đáy là a, chiều cao là h.
Diện tích đáy là: a2.
Diện tích xung quanh là: 4ah
Ta có:V=a2h=4⇒ah=4a(∗)
Lượng vàng cần phải dùng là: a2+4ah=a2+16a
Xét hàm số f(a)=a2+16a,a>0
Ta có: f′(a)=2a−16a2
f′(a)=0⇔2a−16a2=0⇔2a3−16a2=0⇔a=2
Lập bảng biến thiên ta thấy hàm số f(a) đạt giá trị nhỏ nhất tại a=2, thay vào (*) suy ra h=1.