Cho tam giác ABC có cạnh AB=AC, M là trung điểm của BC
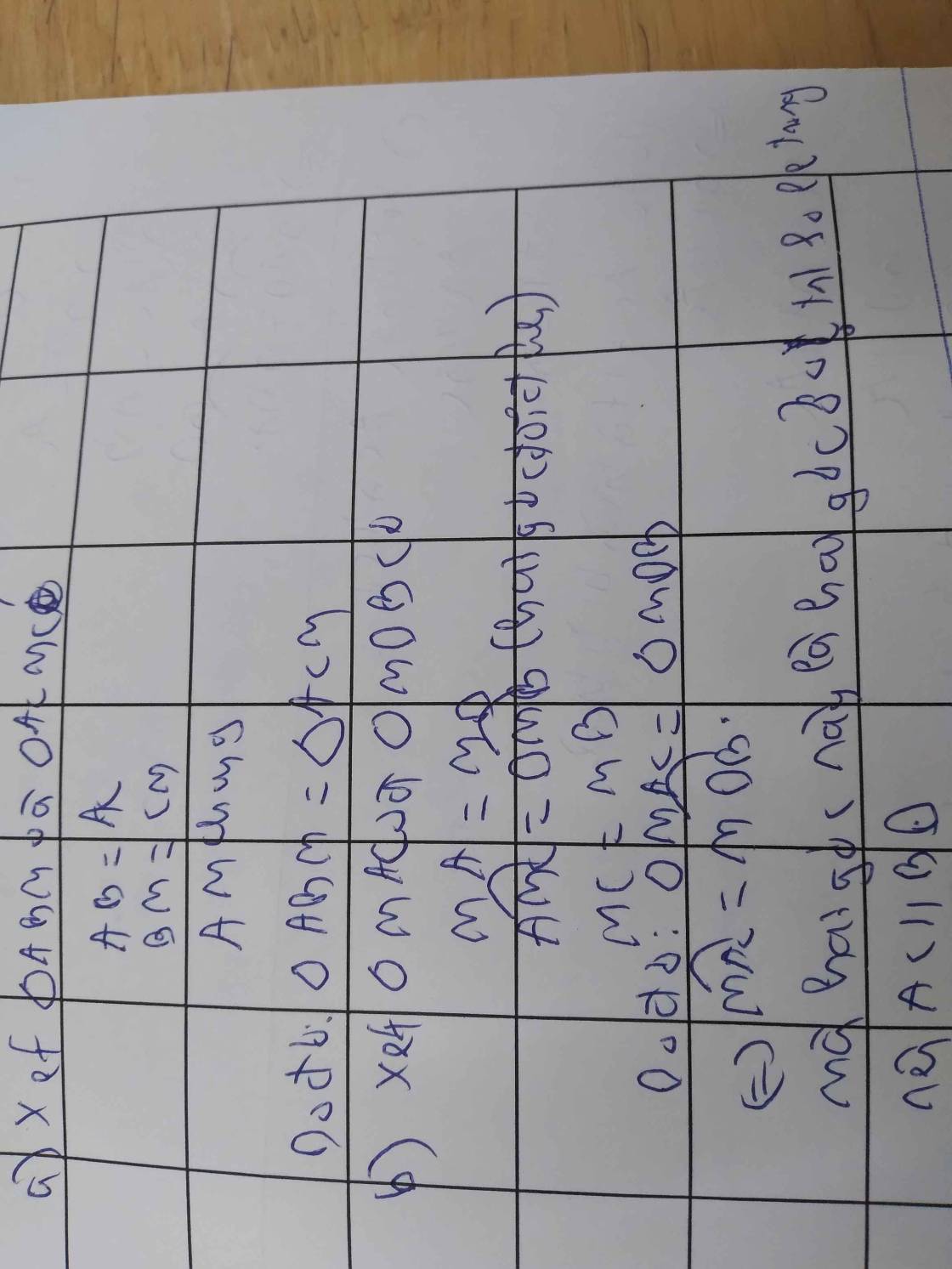
a) Chứng minh tam giác ABM = tam giác ACM
b) Trên tia đối của tia MA lấy điểm D sao cho MD=MA.Chứng minh AC=BD
c) Chứng minh AB song song với CD
d) Trên nửa mặt phẳng bờ là tia AC không chứa điểm B, vẽ tia Ax song song với BC lấy điểm I thuộc Ax sao cho AI=BC. Chứng minh 3 điểm D, C, I thẳng hàng


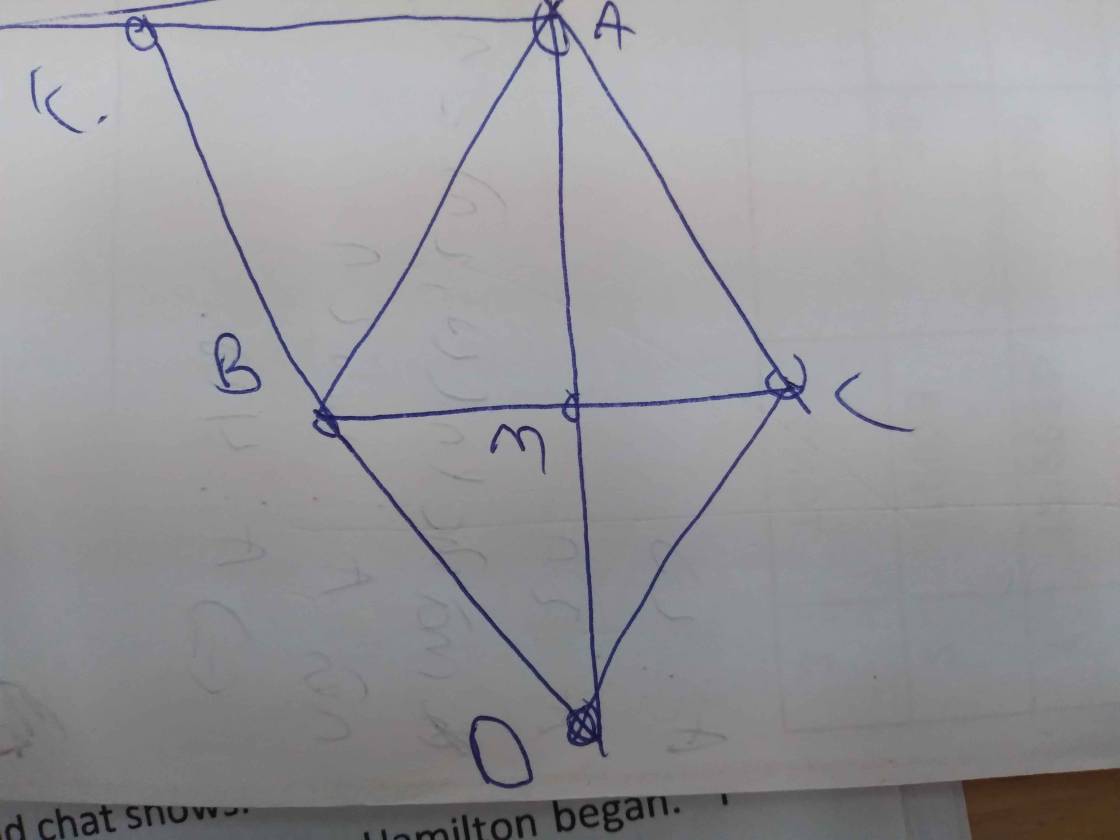

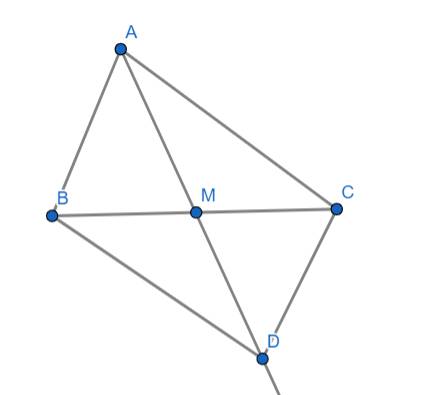
A B C M D
a) Cách 1 :
Xét \(\Delta ABM\) và \(\Delta ACM\) có :
AB = AC (gt)
\(AM:chung\)
\(BM=MC\) (M là trung điểm của BC -gt)
=> \(\Delta ABM=\Delta ACM\left(c.c.c\right)\)
Cách 2 :
Ta có : AB = AC (gt)
=> ΔABC cân tại A
=> \(\widehat{ABC}=\widehat{ACB}\) (tính chất \(\Delta\) cân)
Xét \(\Delta ABM\) và \(\Delta ACM\) có :
\(AB=AC\left(gt\right)\)
\(\widehat{ABM}=\widehat{ACM}\left(cmt\right)\)
\(BM=MC\left(gt\right)\)
=> \(\Delta ABM=\Delta ACM\left(c.g.c\right)\)
Cách 3:
Ta có : M là trung điểm của CB
=> AM là trung tuyến của \(\Delta ABC\)
Mà : \(\Delta ABC\) cân tại A (do AB=AC -gt)
=> AM là đường trung tuyến đồng thời là đường trung trực trong tam giác cân (t/c \(\Delta\) cân)
=> \(AM\perp BC\)
Xét \(\Delta ABM\) và \(\Delta ACM\) có :
\(AB=AC\left(gt\right)\)
\(\widehat{AMB}=\widehat{AMC}\left(=90^{^O}\right)\)- do AM\(\perp\) BC (cmt)
\(BM=MC\left(gt\right)\)
=> \(\Delta ABM=\Delta ACM\) (cạnh huyền-cạnh góc nhọn)
b) Xét △AMC và △DMB có :
\(AM=MD\left(gt\right)\)
\(BM=MC\left(gt\right)\)
\(\widehat{AMC}=\widehat{DMB}\) (đối đỉnh)
=> △AMC = △DMB (c.g.c)
=> AC = BD (Hai cạnh tương ứng)
c) Xét △ABM và △DCM có :
AM = MD (gt)
BM =MC (GT)
\(\widehat{AMB}=\widehat{DMC}\) (đối đỉnh)
=> △ABM = △DCM (c.g.c)
=> \(\widehat{BAM}=\widehat{CDM}\) (2 góc tương ứng)
Mà : Hai góc này ở vị trí so le trong
=> AB//CD