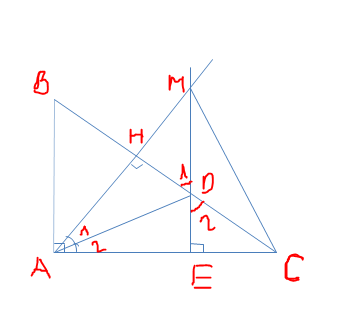
cho tam giác ABC có AB=AC tia phân giác của góc BAC cắt cạnh BC tại H
a) ch/m : tam giác ABH=ACH . từ đó suy ra AH vuông góc BC
b) từ C kẻ đường thẳng vuông góc với AC cắt tia AH tại D , từ D kẻ đường thẳng vuông góc với AD cắt tia AC tại E , kẻ CF vuông góc với DE . trên tia đối của tia FC lấy ddierm G sao cho FC=FG . ch/m: DC=DB=DG
c) ch/m: tam giác BCG vuông
d) ch/m: AB//GE






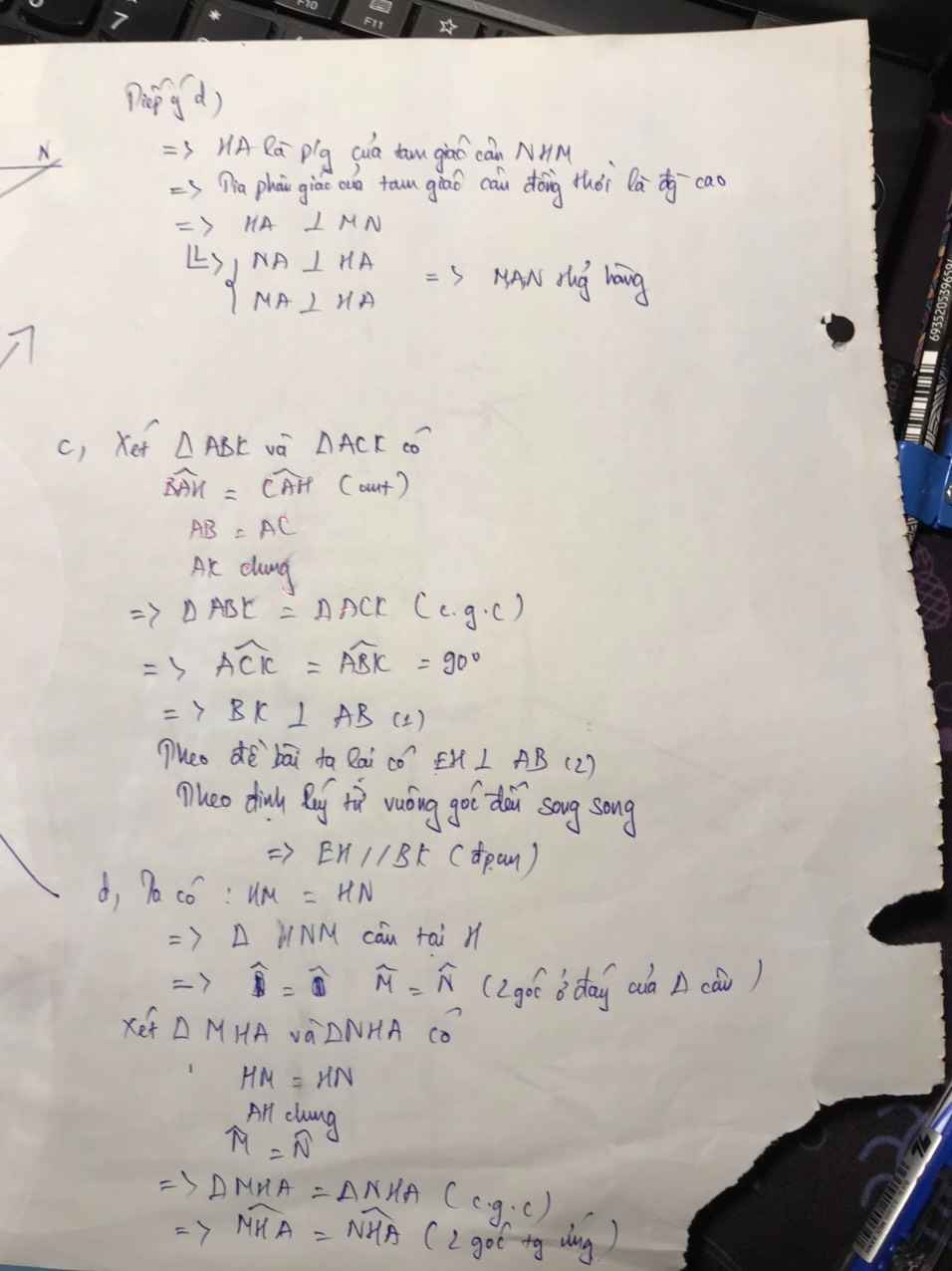


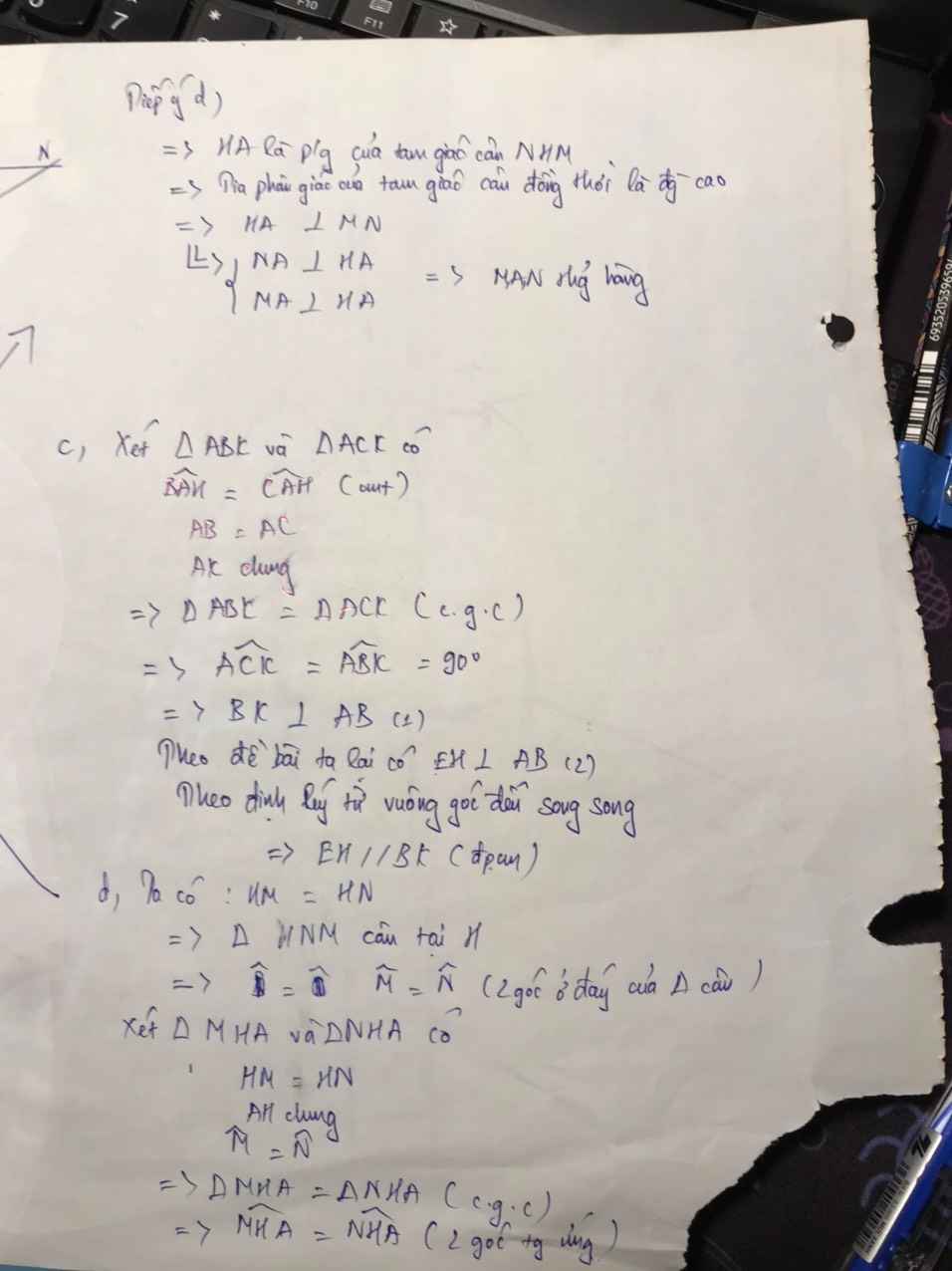


a: Xét ΔABH và ΔACH có
AB=AC
AH chung
HB=HC
Do đó: ΔABH=ΔACH
Ta có: ΔBAC cân tại A
mà AH là đường trung tuyến
nên AH là đường cao
b: Xét ΔABD và ΔACD có
AB=AC
\(\widehat{BAD}=\widehat{CAD}\)
AD chung
Do đó: ΔABD=ΔACD
Suy ra: DB=DC
Xét ΔDCG có
DF là đường cao
DF là đường trung tuyến
Do đó: ΔDCG cân tại D
=>DC=DG