Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét hai tam giác vuông ΔABH ΔABH và ΔACH ΔACH:
Ta có: AH cạnh chung
AB=AC
Vậy ΔABH ΔABH = ΔACH ΔACH (c.g.c)
AH là đường cao đồng thời đường trung tuyến của ΔABC ΔABC cân tại A (AB=AC)
Vậy HC= HB hay H là trung điểm BC
2. BH = HC = BC2= 122 = 6BC2 = 122 = 6 cm
Áp dụng định lí Py-ta-go:
AH = √AB2 − HB2= √102 − 62 = 8AH = AB2− HB2 = 102− 62 = 8 cm
3. Ta có: AK là đường cao ΔAEH ΔAEH
Mà KE = KH nên AK cũng là đường trung tuyến ΔAEH ΔAEH
Vậy ΔAEH ΔAEH cân tại A
Nên AE=AH (1)
4. Ta có: AI là đường cao ΔADH ΔADH
Mà IH = ID nên AI cũng là đường trung tuyến ΔADH ΔADH
Vậy ΔAEH ΔAEH cân tại A
Nên AD = AH (2)
Từ (1)(2) Suy ra: AE=AD hay ΔAED ΔAED cân tại A
5. Xét ΔAEF ΔAEF và ΔADF ΔADF:
Ta có: AF cạnh chung
AE=AD
\(\widehat{AEF}\)=\(\widehat{ADF}\) \(\widehat{AEF}\)=\(\widehat{ADF}\)
Vậy ΔAEFΔAEF =ΔADFΔADF (c.g.c)
Nên EF = FD; AF là đường trung tuyến ΔAED ΔAED cân nên đồng thời đường cao nên AF vuông góc ΔAED ΔAED (3)
AF vuông góc BC (4)
Từ (3)(4) Suy ra: DE//BC
6. Để A là trung điểm ED thì ΔABC ΔABC vuông cân tại A
Giả sử ΔABC ΔABC vuông cân tại A nên AH=HB (đường cao đồng thời trung tuyến) IA=IB (đường cao đồng thời trung tuyến)
Tứ giác ADBH có hai đường chéo cắt nhau tại trung điểm mổi đường nên ADBH là hình bình hành
CM tương tự cho tứ giác AECH
Mà C,H,B thẳng hàng và HC=HB nên E,A,D thẳng hàng và A là trung điểm ED

a) Xét ΔΔABH và ΔΔACH có:
AB = AC (gt)
A1ˆ=A2ˆA1^=A2^ (AH phân giác BACˆBAC^)
AH: chung
=> ΔΔABH = ΔΔACH (c.g.c)
=> {HB=HCAHBˆ=AHCˆ{HB=HCAHB^=AHC^ (ĐN 2 ΔΔ = nhau)
Vì H nằm giữa B, C (gt) và HB = HC (cmt)
=> H trung điểm BC (ĐN trung điểm)
Vì AHBˆ=AHCˆAHB^=AHC^ (cmt)
mà AHBˆ+AHCˆ=180oAHB^+AHC^=180o (2 góc kề bù)
=> AHBˆ=AHCˆ=90oAHB^=AHC^=90o
=> AH ⊥⊥ BC (ĐN 2 đường thẳng ⊥⊥)
b) Vì H trung điểm BC (cmt)
=> HB = HC = BC : 2 (t/c trung điểm) = 12 : 2 = 6cm
Xét ΔΔABH vuông tại H (AHBˆ=90oAHB^=90o) có:
AH2+HB2=AB2AH2+HB2=AB2 (ĐL Pi-ta-go)
=> AH2=AB2−HB2=102−62=64AH2=AB2−HB2=102−62=64
=> AH = 8cm
SABC=12BC⋅AH=12⋅12⋅8=48(cm2)

1: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó: ΔABH=ΔACH
Suy ra: BH=CH
hay H là trung điểm của BC
2: BH=CH=BC/2=6cm
=>AH=8cm
3: Xét ΔAHE có
AK là đường cao
AK là đường trung tuyến
Do đó:ΔAHE cân tại A
hay AH=AE(1)
4: Xét ΔADH có
AI là đường cao
AI là đường trung tuyến
Do đó:ΔADH cân tại A
=>AD=AH(2)
Từ (1) và (2)suy ra AD=AE
hay ΔADE cân tại A
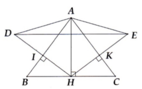




a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó: ΔABH=ΔACH
Suy ra: BH=CH
b: BH=CH=6cm
=>AH=8cm
c: Xét ΔAHE có
AK là đường cao
AK là đường trung tuyến
Do đó: ΔAHE cân tại A
hay AE=AH
d: Xét ΔADH có
AI là đường cao
AI là đườngtrung tuyến
Do đó:ΔADH cân tại A
=>AD=AH=AE
=>ΔADE cân tại A