1-\(\dfrac{1}{3.5}-\dfrac{1}{5.7}-...-\dfrac{1}{53.55}-\dfrac{1}{55.57}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 10 2021
\(\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{99.101}\)
\(=\dfrac{1}{2}\left(\dfrac{2}{1.3}+\dfrac{2}{3.5}+...+\dfrac{2}{99.101}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{99}-\dfrac{1}{101}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{101}\right)=\dfrac{1}{2}.\dfrac{100}{101}=\dfrac{50}{101}\)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
7 tháng 7 2023
Đặt biểu thức là A
\(2A=\dfrac{3-1}{1.3}+\dfrac{5-3}{3.5}+\dfrac{7-5}{5.7}+...+\dfrac{2005-2003}{2003.2005}=\)
\(=1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{2003}-\dfrac{1}{2005}=1-\dfrac{1}{2005}=\dfrac{2004}{2005}\)
\(\Rightarrow A=\dfrac{2004}{2005}:2=\dfrac{1002}{2005}\)
7 tháng 7 2023
Gọi tổng trên là A. Ta có
2A=\(\dfrac{2}{1.3}+\dfrac{2}{3.5}+...+\dfrac{2}{2003.2005}\)
2A=\(\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{2003}-\dfrac{1}{2005}\)
2A=\(\dfrac{1}{1}-\dfrac{1}{2005}=\dfrac{2005}{2005}-\dfrac{1}{2005}=\dfrac{2004}{2005}\)
⇒ A= \(\dfrac{2004}{2005}:2=\dfrac{2004}{2005}.\dfrac{1}{2}=\dfrac{1002}{2005}\)
Vậy tổng trên bằng \(\dfrac{1002}{2005}\)
25 tháng 1 2023
\(B=-\dfrac{1}{2}\cdot\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{99\cdot101}\right)\)
\(=\dfrac{-1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{99}-\dfrac{1}{101}\right)\)
\(=\dfrac{-1}{2}\cdot\dfrac{100}{101}=-\dfrac{50}{101}\)
8 tháng 2 2023
Ta có :
\(\dfrac{1}{1.3}\text{=}2\left(\dfrac{1}{1}-\dfrac{1}{3}\right)\)
\(\dfrac{1}{3.5}\text{=}2\left(\dfrac{1}{3}-\dfrac{1}{5}\right)\)
\(\dfrac{1}{5.7}\text{=}2\left(\dfrac{1}{5}-\dfrac{1}{7}\right)\)
\(...\)
\(\dfrac{1}{2021.2023}\text{=}2\left(\dfrac{1}{2021}-\dfrac{1}{2023}\right)\)
\(\Rightarrow\) biểu thức chỉ còn :
\(2.1-\dfrac{2}{2023}\text{=}\dfrac{4044}{2023}\)
8 tháng 2 2023
đặt biểu thức trên là A
ta có
2A=2/1.3+2/3.5+...+2/2021.2023
2A=1/1-1/3+1/3-1/5+...+1/2021-1/2023
2A=1/1-1/2023
2A=2022/2023
A=(2022/2023):2
A=1011/2023
VD
20 tháng 3 2022
\(j,\dfrac{2}{5.7}+\dfrac{2}{7.9}+...+\dfrac{2}{53.55}=\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+...+\dfrac{1}{53}-\dfrac{1}{55}=\dfrac{1}{5}-\dfrac{1}{55}=\dfrac{11}{55}-\dfrac{1}{55}=\dfrac{10}{55}=\dfrac{2}{11}\\ k,\dfrac{1}{2}.\dfrac{2}{3}.\dfrac{3}{4}.\dfrac{4}{5}...\dfrac{99}{100}=\dfrac{1}{100}.\dfrac{2}{2}.\dfrac{3}{3}...\dfrac{99}{99}=\dfrac{1}{100}.1.1...1=\dfrac{1}{100}\)
V
2
NK
19 tháng 3 2023
\(B=\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{97.99}\)
\(B=\dfrac{1}{1}\cdot\dfrac{1}{3}+\dfrac{1}{3}\cdot\dfrac{1}{5}+\dfrac{1}{5}\cdot\dfrac{1}{7}+...+\dfrac{1}{97}\cdot\dfrac{1}{99}\)
\(B=\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{97}-\dfrac{1}{99}\)
\(B=\dfrac{1}{1}-\dfrac{1}{99}\)
\(B=\dfrac{99}{99}-\dfrac{1}{99}\)
\(B=\dfrac{98}{99}\)
#YVA
H1
22 tháng 3 2023
B=\(\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{97.99}\)
B=\(\left(\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{2}{5.7}+...+\dfrac{2}{97.99}\right):2\)
B=\(\left(\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{97}-\dfrac{1}{99}\right):2\)
B=\(\left(\dfrac{1}{1}-\dfrac{1}{99}\right):2\)
B=\(\dfrac{98}{99}:2\)
B=\(\dfrac{49}{99}\)
NT
6
BD
20 tháng 8 2023
\(\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+\dfrac{1}{5\cdot7}+...+\dfrac{1}{\left(2x-1\right)\cdot\left(2x+1\right)}=\dfrac{49}{99}\)
\(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{\left(2x-1\right)\cdot\left(2x+1\right)}=\dfrac{98}{99}\)
\(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+....+\dfrac{1}{2x-1}-\dfrac{1}{2x+1}=\dfrac{98}{99}\)
\(1-\dfrac{1}{2x+1}=\dfrac{98}{99}\)
\(\dfrac{2x+1-1}{2x+1}=\dfrac{98}{99}\)
\(\dfrac{2x}{2x+1}=\dfrac{98}{99}\)
=> 2x=98
=> x=49
20 tháng 9 2021
\(S=\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+\dfrac{1}{5\cdot7}+\dfrac{1}{7\cdot9}-\left(\dfrac{1}{2\cdot4}+\dfrac{1}{4\cdot6}+\dfrac{1}{6\cdot8}+\dfrac{1}{8\cdot10}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+\dfrac{2}{7\cdot9}\right)-\dfrac{1}{2}\left(\dfrac{2}{2\cdot4}+\dfrac{2}{4\cdot6}+\dfrac{2}{6\cdot8}+\dfrac{2}{8\cdot10}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{9}\right)-\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{10}\right)\)
\(=\dfrac{1}{2}\cdot\dfrac{8}{9}-\dfrac{1}{2}\cdot\dfrac{2}{5}\)
\(=\dfrac{4}{9}-\dfrac{1}{5}\)
\(=\dfrac{11}{45}\)
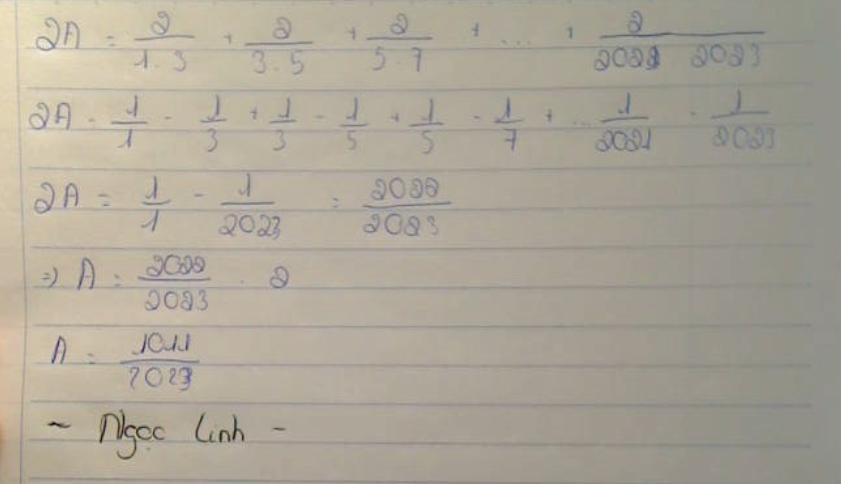
\(=1-\dfrac{1}{2}\left(\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{55\cdot57}\right)\)
\(=1-\dfrac{1}{2}\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{55}-\dfrac{1}{57}\right)\)
\(=1-\dfrac{1}{2}\cdot\dfrac{18}{57}=1-\dfrac{9}{57}=\dfrac{48}{57}=\dfrac{16}{19}\)