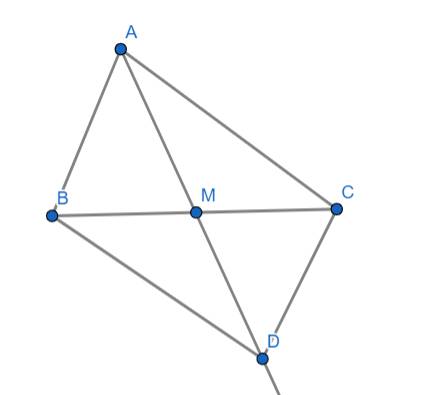
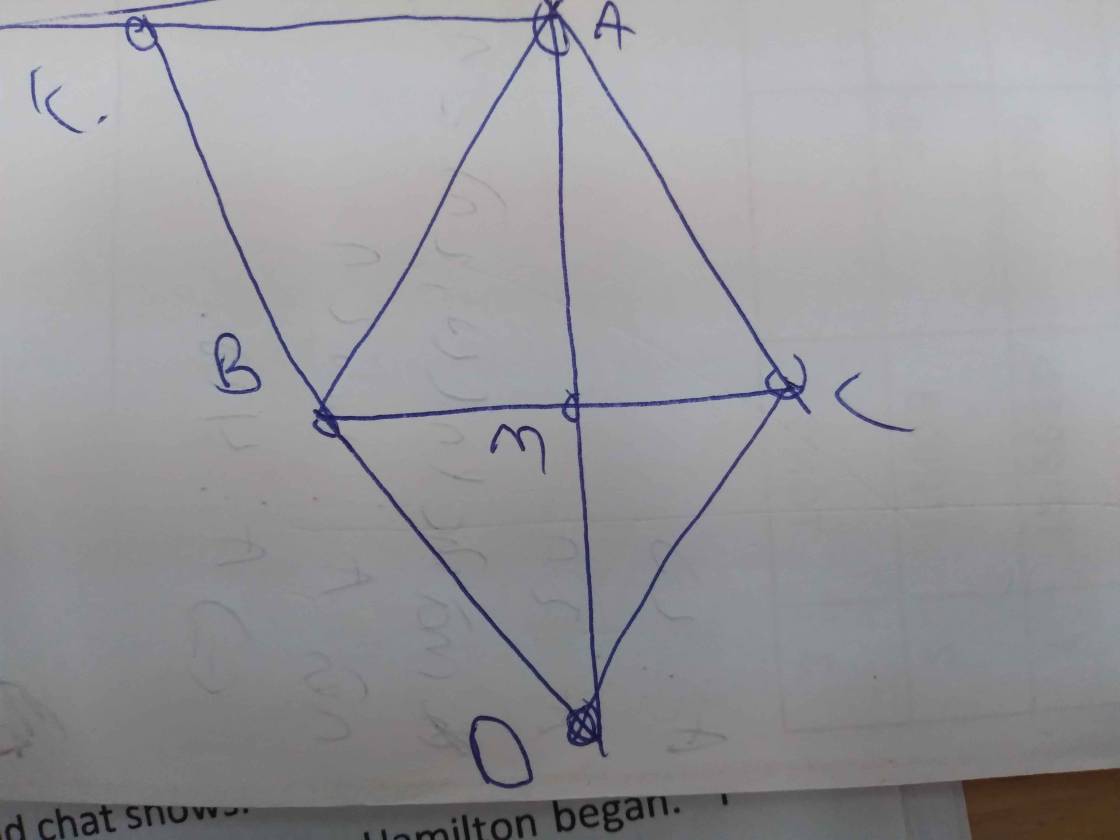
Cho tam giác ABC có cạnh AB=AC,M là trung điểm của BC
a. chứng minh △ABM=△ACM
b. trên tia đối của tia MA lấy điểm D sao cho MD=MA. Chứng minh AC=BD
c. chứng minh AB song song với CD
d. trên nửa mặt phẳng bờ AC không chứa điểm B, vẽ tia Ax song song với BC lấy điểm I ϵ Ax sao cho AI=BC. Chứng minh 3 điểm D,C,I thẳng hàng.

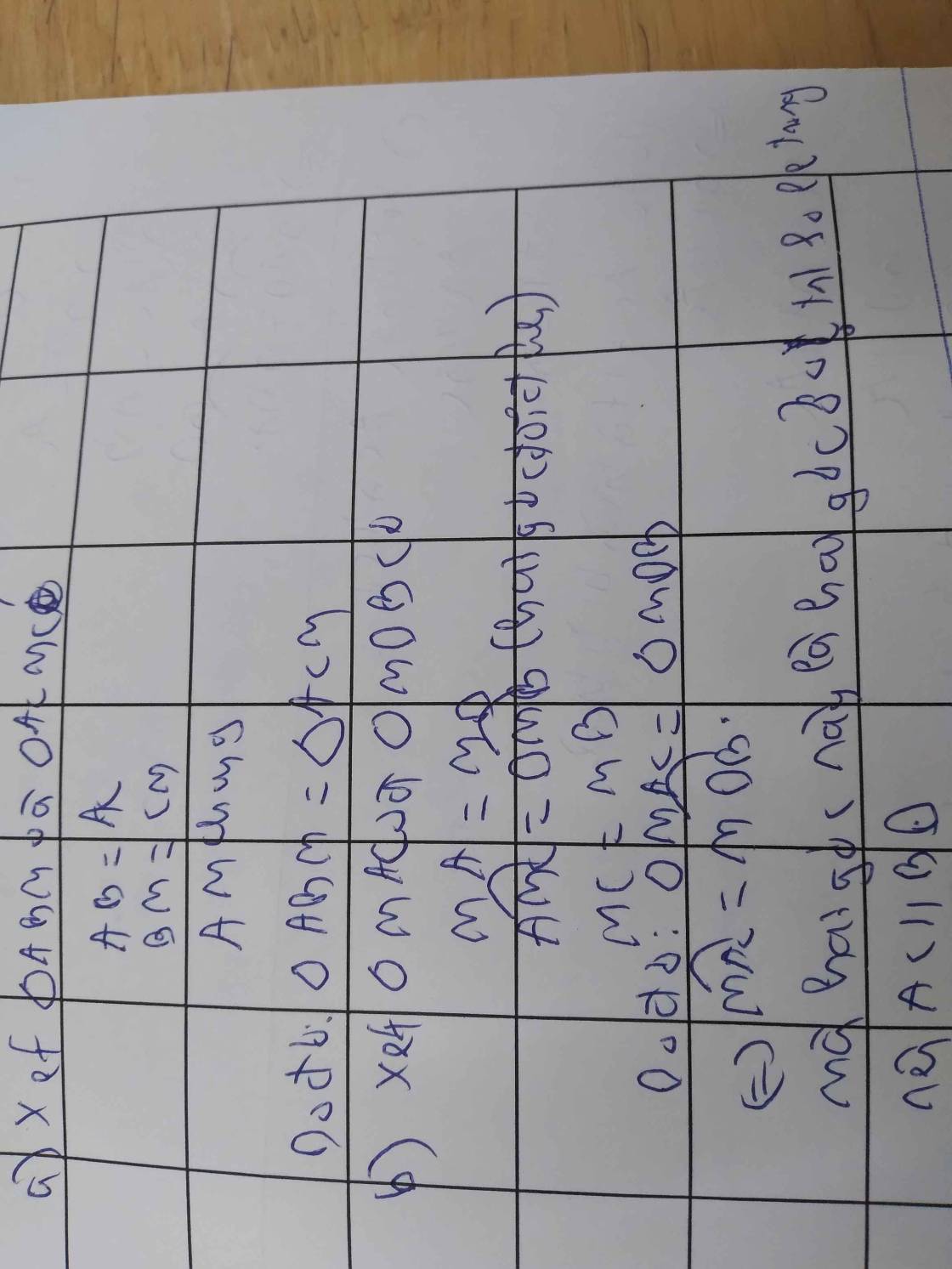

a/ Xét \(\Delta ABM\) và \(\Delta ACM\) có:
\(AM\) cạnh chung
\(AB=AC\left(gt\right)\)
\(MB=MC\) ( M là trung điểm BC )
Do đó \(\Delta ABM=\Delta ACM\left(c.c.c\right)\)
b/ Xét \(\Delta AMC\) và \(\Delta DMB\) có:
\(BM=CM\left(gt\right)\)
\(\widehat{BMD}=\widehat{CMA}\) ( đối đỉnh )
\(MD=MA\left(gt\right)\)
Do đó \(\Delta AMC=\Delta DMB\left(c.g.c\right)\)
\(\Rightarrow AC=BD\) ( cạnh tương ứng )
c/ Vì \(\Delta AMC=\Delta DMB\left(cmt\right)\Rightarrow\widehat{MBD}=\widehat{MCA}\)( góc tương ứng )
Xét hai vị trí này là hai vị trí so le trong mà bằng nhau, suy ra \(AB\text{//}CD\)
a/ Xét ΔABMΔABM và ΔACMΔACM có:
AMAM cạnh chung
AB=AC(gt)AB=AC(gt)
MB=MCMB=MC ( M là trung điểm BC )
Do đó ΔABM=ΔACM(c.c.c)ΔABM=ΔACM(c.c.c)
b/ Xét ΔAMCΔAMC và ΔDMBΔDMB có:
BM=CM(gt)BM=CM(gt)
ˆBMD=ˆCMABMD^=CMA^ ( đối đỉnh )
MD=MA(gt)MD=MA(gt)
Do đó ΔAMC=ΔDMB(c.g.c)ΔAMC=ΔDMB(c.g.c)
⇒AC=BD⇒AC=BD ( cạnh tương ứng )
c/ Vì ΔAMC=ΔDMB(cmt)⇒ˆMBD=ˆMCAΔAMC=ΔDMB(cmt)⇒MBD^=MCA^( góc tương ứng )
Xét hai vị trí này là hai vị trí so le trong mà bằng nhau, suy ra AB//CD
bn hok tốt
mk ko vẽ hik đâu