Phương trình 49x-35x-25x=0 có bao nhiêu nghiệm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
Đặt t = 5 x t > 0
Khi đó PT ⇒ t 2 - m + 2 t + 2 m + 1 = 0 ⇔ t 2 - 2 t + 1 = m t - 2 *
Rõ ràng t = 2 không là nghiệm của phương trình
Do đó * ⇔ m = t 2 - 2 t + 1 t - 2 = t + 1 t - 2 = f t
Xét f(t) trên tập 0 ; 2 ∪ 2 ; + ∞ ta có: f ' t = 1 - 1 t - 2 2 = 0 ⇔ [ t = 1 t = 3
Mặt khác lim x → 0 f t = - 1 2 ; f 1 = 0 ; lim x → 2 - f t = - ∞ ; lim x → 2 + f t = + ∞ ; f 3 = 2 ; lim x → + ∞ f t = + ∞
Lập bảng biến thiên suy ra phương trình có nghiệm khi m ∈ ( - ∞ ; 0 ] ∪ [ 2 ; + ∞ )
Kết hợp m ∈ ℤ và m ∈ 0 ; 2018 suy ra có 2018 giá trị của tham số m.

\(x^4+10x^3+35x^2+50x+21=0\)
\(\Leftrightarrow\left(x^2+5x+3\right)\left(x^2+5x+7\right)=0\)
\(\Leftrightarrow\)\(x^2+5x+3=0\) hoặc \(x^2+5x+7=0\)
\(x^2+5x+3=0\), giải ra ta được 2 nghiệm.
\(x^2+5x+7\ge\frac{3}{4}\), vô nghiệm.
Vậy phương trình có 2 nghiệm.

a) 35x2– 37x + 2 = 0 có a = 0, b = -37, c = 2
Do đó: a + b + c = 35 + (-37) + 2 = 0
nên x1 = 1; x2 = \(\dfrac{2}{35}\)
b) 7x2 + 500x - 507 = 0 có a = 7, b = 500, c = -507
Do đó: a + b + c = 7 + 500 - 507
nên x1 = 1; x2 = \(-\dfrac{507}{7}\)
c) x2- 49x - 50 = 0 có a = 1, b = -49, c = -50
Do đó a - b + c = 1 - (-49) - 50 = 0
nên x1 = -1; x2 = \(-\dfrac{-50}{1}\) = 50
d) 4321x2 + 21x - 4300 = 0 có a = 4321, b = 21, c = -4300
Do đó a - b + c = 4321 - 21 + (-4300) = 0
nên x1 = -1; x2 = \(\dfrac{-4300}{4321}\) = \(\dfrac{4300}{4321}\).
a) 35x2– 37x + 2 = 0 có a = 0, b = -37, c = 2
Do đó: a + b + c = 35 + (-37) + 2 = 0
nên x1 = 1; x2 =
b) 7x2 + 500x - 507 = 0 có a = 7, b = 500, c = -507
Do đó: a + b + c = 7 + 500 - 507
nên x1 = 1; x2 =
c) x2- 49x - 50 = 0 có a = 1, b = -49, c = -50
Do đó a - b + c = 1 - (-49) - 50 = 0
nên x1 = -1; x2 = = 50
d) 4321x2 + 21x - 4300 = 0 có a = 4321, b = 21, c = -4300
Do đó a - b + c = 4321 - 21 + (-4300) = 0
nên x1 = -1; x2 = =
.

\(x^3-6x^2-25x-18=0\)
\(\Leftrightarrow x^2\left(x+1\right)-7x\left(x+1\right)-18\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2-7x-18\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+2x-9x-18\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left[x\left(x+2\right)-9\left(x+2\right)\right]=0\)
\(\Leftrightarrow\left(x+1\right)\left(x+2\right)\left(x-9\right)=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x+1=0\\x+2=0\\x-9=0\end{array}\right.\Leftrightarrow\left[\begin{array}{nghiempt}x=-1\\x=-2\\x=9\end{array}\right.\)
Vậy nghiệm nhỏ nhất của phương trình là \(-2\)

Đáp án A
P T ⇔ 5 2 2 x − 2 5 2 x + m 2 = 0 → t − 5 2 x t 2 − 2 t + m 2 = 0 1 .
PT ban đầu có 2 nghiệm trái dấu ⇔ 1 có hai nghiệm thỏa mãn 0 < t 1 < 1 < t 2 .
Suy ra Δ ' 1 > 0 t 1 + t 2 > 0 t 1 t 2 > 0 t 1 − 1 t 2 − 1 < 0 ⇔ 1 − m 2 > 0 2 > 0 m 2 > 0 t 1 t 2 − t 1 + t 2 + 1 < 0
⇔ − 1 < m < 1 m ≠ 0 m 2 − 2 + 1 < 0 ⇔ − 1 < m < 1 m ≠ 0 .
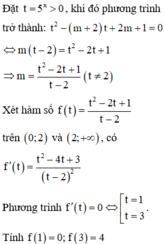





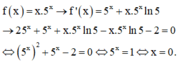
Lời giải:
Ta có:
\(49^x-35^x-25^x=0\)
\(\Leftrightarrow \frac{49^x}{25^x}-\frac{35^x}{25^x}-1=0\)
\(\Leftrightarrow \left(\frac{7}{5}\right)^{2x}-\left(\frac{7}{5}\right)^x-1=0\)
Đặt \(\left(\frac{7}{5}\right)^x=t\Rightarrow t^2-t-1=0\)
Ta thấy \(\Delta=5>0\Rightarrow t^2-t-1=0\) có hai nghiệm phân biệt
Theo hệ thưc Viete với $t_1,t_2$ là hai nghiệm của pt thì \(t_1t_2=-1<0 \) , do đó pt có hai nghiệm trái dấu. Vì $t>0$ nên chỉ có một nghiệm thỏa mãn.
Chỉ có một $t$ thỏa mãn đồng nghĩa với việc chỉ có một giá trị $x$ thỏa mãn
Vậy phương trình ban đầu có một nghiệm.