Cho tam giác ABC, giả sử AD và AE lần lượt là các đường phân giác trong và phân giác ngoài tại đỉnh A của tam giác. Chứng minh rằng , khi độ dài các cạnh của tam giác ABC thay đổi thỏa mãn 3AB=2AC thì BD/BE không đổi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


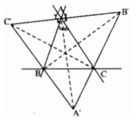
Ta có AA′⊥ AB′ vì chúng là hai tia phân giác của hai góc kề bù. Tương tự AA′⊥ AC′. Vì qua A chỉ có một đường vuông góc với AA' nên ba điểm B', A, C' thẳng hàng và AA′⊥ B′C′, hay A'A là một đường cao của tam giác A'B'C'. Hoàn toàn tương tự ta chứng minh được BB' và CC' là hai đường cao của tam giác A'B'C'.
Mặt khác theo cách chứng minh của bài 9.5 ta có AA', BB', CC' là ba tia phân giác của các góc A, B, C của tam giác ABC. Từ đó suy ra giao điểm của ba đường phân giác của tam giác ABC là trực tâm của tam giác A'B'C'.

a, Do DE//BC
=> \(\widehat{A_1}=\widehat{ABC}\)( so le trong )
Vì \(\widehat{BAz}\)là góc ngoài tam giác ABC
=> \(\widehat{BAz}=\widehat{ABC}+\widehat{ACB}\)
\(\Rightarrow\widehat{A_1}+\widehat{A_2}=\widehat{ABC}+\widehat{ACB}\)
Do \(\widehat{A_1}=\widehat{ABC}\)( chứng minh trên )
\(\Rightarrow\widehat{A_2}=\widehat{ACB}\)
Mà góc ABC = góc ACB ( tam giác ABC cân ở A )
=> \(\widehat{A_1}=\widehat{A_2}\)
=> Ax là tia phân giác góc BAz
Hay Ax là phân giác góc ngoài đỉnh A của tam giác ABC
b, Vì \(\widehat{A_2}=\widehat{CAE}\)( 2 góc đối đỉnh)
Mà \(\widehat{A_2}=\widehat{A_1}\)(cmt)
\(\Rightarrow\widehat{A_1}=\widehat{CAE}\)
\(\Rightarrow\widehat{A_1}+\widehat{BAC}=\widehat{CAE}+\widehat{BAC}\)
\(\Rightarrow\widehat{DAC}=\widehat{EAB}\)
Vì góc ABC = góc ACB ( tam giác ABC cân )
=> \(\frac{1}{2}\widehat{ABC}=\frac{1}{2}\widehat{ACB}\Rightarrow\widehat{ABE}=\widehat{ACD}\)
Xét tam giác DAC và tam giác EAB có:
\(\widehat{ACD}=\widehat{ABE}\)( chứng minh trên )
AC = AB ( tam giác ABC cân )
\(\widehat{DAC}=\widehat{EAB}\)( chứng minh trên )
=> \(\Delta DAC=\Delta EAB\)( g-c-g )
=> DA = EA