cho tam giác ABC có AB=AC.H là trung điểm của BC.Trên tia đối của HA lấy K sao cho KH=AH.Chứng Minh rằng a,tam giác ABH=tam giác ACH b,AH\(\perp\)BC c,CK//AB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 9 2018
( hình vẽ và GTKL tự làm)
a) xét \(\Delta ABH\)và\(\Delta ACH\)có :
\(AB=AC\)\(\left(GT\right)\)
\(BH=CH\left(GT\right)\)\(\Rightarrow\Delta ABH=\Delta ACH\left(c.c.c\right)\)
\(AH\)\(chung\)
b) Ta có \(AHB=AHC\)( 2 góc tương ứng )
.Mà \(AHB+AHC=180\)O
\(\Rightarrow AHB=AHC=90\)O
\(\Rightarrow AH\perp BC\)
C) Xét 2 \(\Delta AHB\)và\(KHC\)có :
\(BH=CH\)\(\left(GT\right)\)
\(KH=AH\left(GT\right)\)
\(BHA=CHK\)( ĐỐI ĐỈNH )
\(\Rightarrow\Delta AHB=\Delta KHC\left(c.g.c\right)\)
\(\Rightarrow ABH=KCH\)( 2 góc tương ứng )
Mà 2 góc này so le trong
\(\Rightarrow CK//AB\)
S
19 tháng 12 2022
a) xét ΔABH và ΔACH, ta có :
AB = AC (giả thiết)
\(\widehat{ABC}=\widehat{ACB}\) (vì AB = AC => đó là tam giác cân, mà tam giác cân thì có 2 góc ở đáy bằng nhau)
AH là cạnh chung
ð ΔABH = ΔACH (c.c.c)
b) vì ΔABH = ΔACH, nên :
=> HB = HC (2 cạnh tương ứng)
c) hơi khó nha !
1 tháng 3 2021
a) Xét ΔABH và ΔACH có
AB=AC(ΔABC cân tại A)
\(\widehat{BAH}=\widehat{CAH}\)(AH là tia phân giác của \(\widehat{BAC}\))
AH chung
Do đó: ΔABH=ΔACH(c-g-c)
b) Ta có: ΔABH=ΔACH(cmt)
nên BH=CH(hai cạnh tương ứng)
Xét ΔABH và ΔKCH có
BH=CH(cmt)
\(\widehat{AHB}=\widehat{CHK}\)(hai góc đối đỉnh)
AH=KH(gt)
Do đó: ΔABH=ΔKCH(c-g-c)
Suy ra: \(\widehat{BAH}=\widehat{CKH}\)(hai góc tương ứng)
mà \(\widehat{BAH}\) và \(\widehat{CKH}\) là hai góc ở vị trí so le trong
nên AB//CK(Dấu hiệu nhận biết hai đường thẳng song song)
c) Sửa đề: I là trung điểm của DC
Ta có: AB=AC(ΔABC cân tại A)
mà AB=AD(Gt)
nên AC=AD
Xét ΔACI và ΔADI có
AC=AD(cmt)
AI chung
CI=DI(I là trung điểm của DC)
Do đó: ΔACI=ΔADI(c-c-c)
d) Ta có: ΔACI=ΔADI(cmt)
nên \(\widehat{AIC}=\widehat{AID}\)(hai góc tương ứng)
mà \(\widehat{AIC}+\widehat{AID}=180^0\)(hai góc kề bù)
nên \(\widehat{AIC}=\widehat{AID}=\dfrac{180^0}{2}=90^0\)
hay AI⊥CD(1)
Ta có: AB=AD(gt)
mà B,A,D thẳng hàng(gt)
nên A là trung điểm của BD
Xét ΔCBD có
CA là đường trung tuyến ứng với cạnh BD(A là trung điểm của BD)
\(CA=\dfrac{BD}{2}\left(CA=AB=\dfrac{BD}{2}\right)\)
Do đó: ΔCBD vuông tại C(Định lí)
⇒BC⊥CD(2)
Từ (1) và (2) suy ra AI//BC(Đpcm)
VN
22 tháng 12 2016
a) Xét tam giác ABC có AB = AC => Tam giác ABC cân tại A
=> AH vừa là đường trung tuyến vừa là tia phân giác góc BAC
b) Vì tam giác ABC cân tại A (cmt)
=> AH cũng là đường cao
=> AH vuông góc BC
c) Xét tứ giác ABCK có
H là trung điểm BC (gt)
H là trung điểm AK (gt)
=> Tứ giác ABCK là hình bình hành
=> CK // AB
3 tháng 10 2021
a: Xét ΔABH và ΔACH có
AB=AC
AH chung
BH=CH
Do đó: ΔABH=ΔACH
Suy ra: \(\widehat{BAH}=\widehat{CAH}\)
hay AH là tia phân giác của \(\widehat{BAC}\)
b: Ta có: AB=AC
nên A nằm trên đường trung trực của BC(1)
Ta có: HB=HC
nên H nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra AH là đường trung trực của BC
hay AH\(\perp\)BC
30 tháng 11 2015
bạn bấm vào chữ xanh này!
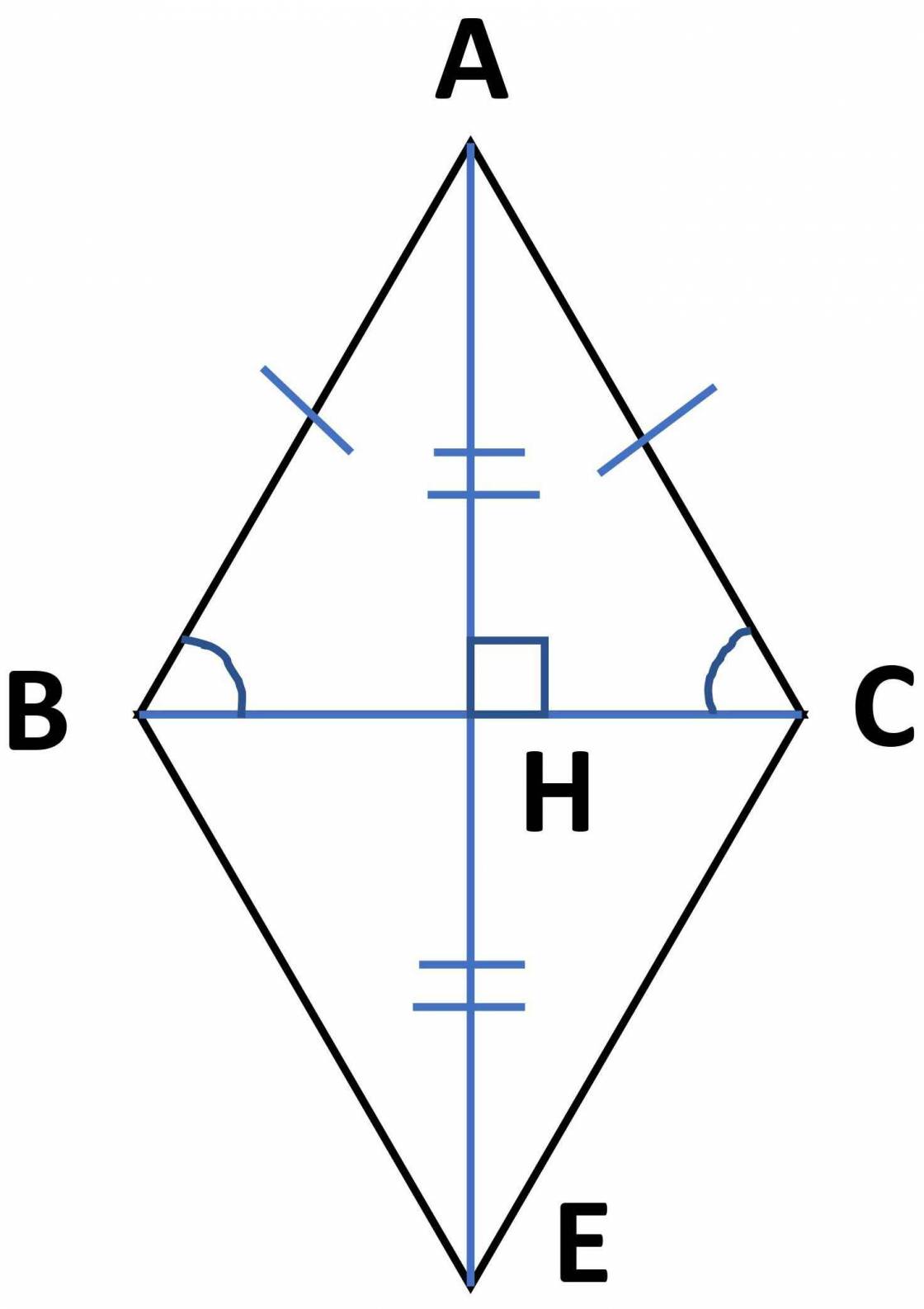
cho tam giác ABC có AB=AC. Gọi H la trung điểm của canh BC.a. Chứng minh AH là tia phân giác của góc BAC và AH vuông góc BC ?b.Trên tia đối của tia HA lấy K sao cho HK=HA.Chứng minh rằng CK song song với AB A B C H K
a, vì AH là trung diểm của BC nên ∆ABH=∆ACH
b,∆ABH=∆ACH và AH là trung diểm của BC nên AH vuông góc với BC
c,vì AH vuông góc với BC và ∆ABH=∆ACH => CK//AB
Hình thì sao bạn