Một kiện hàng có 20 sản phẩm trong đó có 16 sản phẩm loại I và 4 sản phẩm loại II. Lần lượt chọn ngẫu nhiên ra 3 sản phẩm từ kiện hàng. Tính xác suất để sản phẩm chọn lần ba là loại II biết rằng trong hai sản phẩm chọn ra từ lần thứ nhất và lần thứ hai có một sản phẩm loại I và một sản phẩm loại II.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 12 2021
Gọi A là biến cố "sản phẩm chọn được từ lô 2 là loại A"
\(B_1\) là biến cố "viên bi được lấy ra là viên của hộp 1" \(\Rightarrow P\left(B_1\right)=\dfrac{C_5^1}{C_{20}^1}=\dfrac{1}{4}\)
\(B_2\) là biến cố "viên bi được lấy ra là viên bi của hộp 2" \(\Rightarrow P\left(B_2\right)=\dfrac{C_{15}^1}{C_{20}^1}=\dfrac{3}{4}\)
\(P\left(A|B_1\right)=\dfrac{C_3^1}{C_7^1}=\dfrac{3}{7}\)
\(P\left(A|B_2\right)=\dfrac{C_9^1}{C_{15}^1}=\dfrac{3}{5}\)
Xác suất:
\(P\left(A\right)=\dfrac{1}{4}.\dfrac{3}{7}+\dfrac{3}{4}.\dfrac{3}{5}=\dfrac{39}{70}\)
HQ
Hà Quang Minh
Giáo viên
28 tháng 9 2023
a) Số kết quả xảy ra khi chọn ngẫu nhiên 3 sản phẩm là: \(C_{20}^3\) ( kết quả )
b) Chọn ngẫu nhiên 3 sản phẩm từ 20 sản phẩm ta được một tổ hợp chập 3 của 20. Do đó, số phần tử của không gian mẫu là: \(n\left( \Omega \right) = C_{20}^3\)( phần tử)
Gọi A là biến cố “Cả 3 sản phẩm được chọn là chính phẩm”
Để chọn được cả 3 sản phẩm đều là chính phẩm thì ta phải chọn 3 sản phẩm từ 16 chính phẩm tức là ta được một tổ hợp chập 3 của 16 phần tử. Do đó số phần tử của biến cố A là: \(n\left( A \right) = C_{16}^3\)( phần tử)
Vậy xác suất của biến cố A là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{C_{16}^3}}{{C_{20}^3}} = \frac{{28}}{{57}}\).
CM
4 tháng 9 2018
Chọn D
Số phần tử không gian mấu bằng số cách lấy ra 4 sản phẩm từ 20 sản phẩm là: C 20 4 (cách)
Cách 1: Để lấy ra 4 sản phẩm có sản phẩm lỗi ta chia các trường hợp:
TH1: Lấy được 3 sản phẩm tốt và 1 sản phẩm lỗi, ta có: C 18 3 . C 2 1 (cách)
TH2: Lấy được 2 sản phẩm tốt và 2 sản phẩm lỗi, ta có: C 18 2 . C 2 2 (cách)
Vậy xác suất cần tìm là: 
Cách 2: Xét biến cố đối:
Số cách lấy ra 4 sản phẩm không có sản phẩm lỗi C 18 4 (cách)
Vậy xác suất cần tìm là: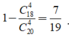 
HT
13 tháng 3 2021
1/
a/ TH1: Lấy 1 sp loại A từ lô I có: \(C^1_3\) (cách)
Lấy 1 sp từ 4 sp còn lại từ lô II có: \(C^1_4\) (cách)
\(\Rightarrow C^1_3.C^1_4\) (cách)
TH2: Lấy 1 sp loại A từ lô II có: \(C^1_6\) (cách)
Lấy 1 sp từ 7 sp còn lại từ lô I có: \(C^1_7\) (cách)
\(\Rightarrow C^1_6.C^1_7\) (cách)
Không gian mẫu: \(n\left(\Omega\right)=C^1_{10}.C^1_{10}\)
\(\Rightarrow p\left(M\right)=\dfrac{C^1_6.C^1_7+C^1_3.C^1_4}{C_{10}^1.C^1_{10}}=0,54\)
b/ TH1: Lấy 1 sp loại A từ lô I: \(C^1_3\) (cách)
Lấy 1 sp loại A từ lô II: \(C^1_6\) (cách)
\(\Rightarrow C^1_3.C^1_6\) (cách)
TH2: Lấy 1 sp từ 7 sp còn lại trong lô I: \(C^1_7\) (cách)
Lấy 1 sp từ 4 sp còn lại trong lô II: \(C^1_4\) (cách)
\(\Rightarrow C^1_7.C^1_4\) (cách)
\(\Rightarrow p\left(O\right)=\dfrac{C_3^1.C_6^1+C^1_7.C^1_4}{C^1_{10}.C^1_{10}}=...\)
Bài 2 mình ko chắc nên ko làm nhé :(
CM
14 tháng 9 2017
Chọn D
Ta có: 
Gọi A là biến cố lấy ra 3 sản phẩm trong đó có ít nhất một sản phẩm tốt.
=>
A
¯
là biến cố lấy ra 3 sản phẩm không có sản phẩm tốt và 
Vậy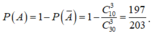 
CM
16 tháng 6 2019
Đáp án B
Gọi A là biến cố: “ 3 sản phẩm lấy ra có ít nhất một sản phẩm tốt”
Khi đó 
là biến cố :”3 sản phẩm lấy ra không có sản phẩm nào tốt”
Ta có:
Suy ra 
Lời giải:
Lấy lần 1 và lần 2 đã lấy ra được 1 sản phẩm loại I và 1 sản phẩm loại II, do đó còn $15$ sản phẩm loại I và $3$ sản phẩm loại II (tổng 18 sản phẩm)
Trong lần thứ 3:
Lấy ngẫu nhiên 1 sản phẩm, có $C^1_18=18$ cách chọn
Lấy ngẫu nhiên 1 sản phẩm loại II từ 3 sản phẩm loại II, có $C^1_3=3$ cách chọn
Xác suất để lấy được sản phẩm loại II: $\frac{3}{18}=\frac{1}{6}$
dạ, em cám ơn Thầy ạ