Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
1/
a/ TH1: Lấy 1 sp loại A từ lô I có: \(C^1_3\) (cách)
Lấy 1 sp từ 4 sp còn lại từ lô II có: \(C^1_4\) (cách)
\(\Rightarrow C^1_3.C^1_4\) (cách)
TH2: Lấy 1 sp loại A từ lô II có: \(C^1_6\) (cách)
Lấy 1 sp từ 7 sp còn lại từ lô I có: \(C^1_7\) (cách)
\(\Rightarrow C^1_6.C^1_7\) (cách)
Không gian mẫu: \(n\left(\Omega\right)=C^1_{10}.C^1_{10}\)
\(\Rightarrow p\left(M\right)=\dfrac{C^1_6.C^1_7+C^1_3.C^1_4}{C_{10}^1.C^1_{10}}=0,54\)
b/ TH1: Lấy 1 sp loại A từ lô I: \(C^1_3\) (cách)
Lấy 1 sp loại A từ lô II: \(C^1_6\) (cách)
\(\Rightarrow C^1_3.C^1_6\) (cách)
TH2: Lấy 1 sp từ 7 sp còn lại trong lô I: \(C^1_7\) (cách)
Lấy 1 sp từ 4 sp còn lại trong lô II: \(C^1_4\) (cách)
\(\Rightarrow C^1_7.C^1_4\) (cách)
\(\Rightarrow p\left(O\right)=\dfrac{C_3^1.C_6^1+C^1_7.C^1_4}{C^1_{10}.C^1_{10}}=...\)
Bài 2 mình ko chắc nên ko làm nhé :(
Chọn D
Ta có: 
Gọi A là biến cố lấy ra 3 sản phẩm trong đó có ít nhất một sản phẩm tốt.
=>
A
¯
là biến cố lấy ra 3 sản phẩm không có sản phẩm tốt và 
Vậy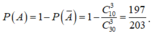 
Đáp án B
Gọi A là biến cố: “ 3 sản phẩm lấy ra có ít nhất một sản phẩm tốt”
Khi đó 
là biến cố :”3 sản phẩm lấy ra không có sản phẩm nào tốt”
Ta có:
Suy ra 
Chọn D
Số phần tử không gian mấu bằng số cách lấy ra 4 sản phẩm từ 20 sản phẩm là: C 20 4 (cách)
Cách 1: Để lấy ra 4 sản phẩm có sản phẩm lỗi ta chia các trường hợp:
TH1: Lấy được 3 sản phẩm tốt và 1 sản phẩm lỗi, ta có: C 18 3 . C 2 1 (cách)
TH2: Lấy được 2 sản phẩm tốt và 2 sản phẩm lỗi, ta có: C 18 2 . C 2 2 (cách)
Vậy xác suất cần tìm là: 
Cách 2: Xét biến cố đối:
Số cách lấy ra 4 sản phẩm không có sản phẩm lỗi C 18 4 (cách)
Vậy xác suất cần tìm là: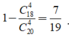 
Lời giải:
Lấy lần 1 và lần 2 đã lấy ra được 1 sản phẩm loại I và 1 sản phẩm loại II, do đó còn $15$ sản phẩm loại I và $3$ sản phẩm loại II (tổng 18 sản phẩm)
Trong lần thứ 3:
Lấy ngẫu nhiên 1 sản phẩm, có $C^1_18=18$ cách chọn
Lấy ngẫu nhiên 1 sản phẩm loại II từ 3 sản phẩm loại II, có $C^1_3=3$ cách chọn
Xác suất để lấy được sản phẩm loại II: $\frac{3}{18}=\frac{1}{6}$
dạ, em cám ơn Thầy ạ