lm giúp mình với ạ
K
Khách
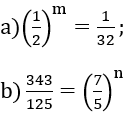
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 3 2023
Câu 18:
PT: \(Zn+2HCl\rightarrow ZnCl_2+H_2\)
\(n_{Zn}=\dfrac{6,5}{65}=0,1\left(mol\right)\)
\(n_{HCl}=0,15.2=0,3\left(mol\right)\)
Xét tỉ lệ: \(\dfrac{0,1}{1}< \dfrac{0,3}{2}\), ta được HCl dư.
Theo PT: \(n_{ZnCl_2}=n_{H_2}=n_{Zn}=0,1\left(mol\right)\)
\(\Rightarrow V_{H_2}=0,1.22,4=2,24\left(l\right)\)
\(C_{M_{ZnCl_2}}=\dfrac{0,1}{0,15}=\dfrac{2}{3}\left(M\right)\)
H9
HT.Phong (9A5)
CTVHS
28 tháng 10 2023
Bài 2:
\(A=2+2^2+2^3+...+2^{60}\)
\(A=\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{59}+2^{60}\right)\)
\(A=2\cdot\left(1+2\right)+2^3\cdot\left(1+2\right)+...+2^{59}\cdot\left(1+2\right)\)
\(A=2\cdot3+2^3\cdot3+...+2^{59}\cdot3\)
\(A=3\cdot\left(2+2^3+...+2^{59}\right)\) ⋮ 3
Vậy: A ⋮ 3
_____________
\(A=2+2^2+...+2^{60}\)
\(A=\left(2+2^2+2^3\right)+\left(2^4+2^5+2^6\right)+...+\left(2^{58}+2^{59}+2^{60}\right)\)
\(A=2\cdot\left(1+2+4\right)+2^4\cdot\left(1+2+4\right)+...+2^{58}\cdot\left(1+2+4\right)\)
\(A=2\cdot7+2^4\cdot7+...+2^{58}\cdot7\)
\(A=7\cdot\left(2+2^4+....+2^{58}\right)\) ⋮ 7
Vậy: A ⋮ 7
___________________
\(A=2+2^2+...+2^{60}\)
\(A=\left(2+2^3\right)+\left(2^2+2^4\right)+...+\left(2^{58}+2^{60}\right)\)
\(A=2\cdot\left(1+4\right)+2^2\cdot\left(1+4\right)+...+2^{58}\cdot\left(1+4\right)\)
\(A=2\cdot5+2^2\cdot5+...+2^{58}\cdot5\)
\(A=5\cdot\left(2+2^2+...+2^{58}\right)\) ⋮ 5
Vậy: A ⋮ 5
29 tháng 8 2021
a: Ta có: \(\sqrt{x^2-4x+4}=\sqrt{4x^2-12x+9}\)
\(\Leftrightarrow\left|x-2\right|=\left|2x-3\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=x-2\\2x-3=2-x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{5}{3}\end{matrix}\right.\)
29 tháng 8 2021
c: Ta có: \(\sqrt{4x^2-4x+1}=\sqrt{x^2-6x+9}\)
\(\Leftrightarrow\left|2x-1\right|=\left|x-3\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=x-3\\2x-1=3-x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{4}{3}\end{matrix}\right.\)
PN
1
13 tháng 2
đây mà là thủ công á bạn đây là toán chớ nhìn trông khoai ghê cố lên nha có nghĩ đi ,chớ khó quá luôn mik ko giải đc.chúc bạn giải đc j nha !!!!!!!!!!!
1 tháng 9 2021
\(\dfrac{1}{\sqrt{\dfrac{5}{7}}+\sqrt{\dfrac{5}{13}}+1}+\dfrac{1}{\sqrt{\dfrac{7}{13}}+\sqrt{\dfrac{7}{5}}+1}+\dfrac{1}{\sqrt{1\dfrac{6}{7}}+\sqrt{2\dfrac{3}{5}}+1}\\ =\dfrac{1}{\dfrac{\sqrt{5}}{\sqrt{7}}+\dfrac{\sqrt{5}}{\sqrt{13}}+\dfrac{\sqrt{5}}{\sqrt{5}}}+\dfrac{1}{\dfrac{\sqrt{7}}{\sqrt{13}}+\dfrac{\sqrt{7}}{\sqrt{5}}+\dfrac{\sqrt{7}}{\sqrt{7}}}+\dfrac{1}{\dfrac{\sqrt{13}}{\sqrt{7}}+\dfrac{\sqrt{13}}{\sqrt{5}}+\dfrac{\sqrt{13}}{\sqrt{13}}}\\ =\left(\dfrac{1}{\sqrt{5}}+\dfrac{1}{\sqrt{7}}+\dfrac{1}{\sqrt{13}}\right)\cdot\dfrac{1}{\dfrac{1}{\sqrt{5}}+\dfrac{1}{\sqrt{7}}+\dfrac{1}{\sqrt{13}}}\\ =1\)
a) \(\left(\frac{1}{2}\right)^5=\frac{1}{32}\)
b) \(\frac{343}{125}=\left(\frac{7}{5}\right)^3\)