Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a,b:
Xét tứ giác ABCE có
BC//AE
BC=AE
Do đó: ABCE là hình bình hành
mà BC=BA
nên ABCE là hình thoi
Xét tứ giác BCDE có
BC//DE
BC=DE
Do đó: BCDE là hình bình hành
mà CB=CD
nên BCDE là hình thoi
Xét ΔCED có CE=ED
nên ΔCED cân tại E
mà CE=CD
nên ΔCED đều
=>\(\widehat{C}=60^0\)
Gọi F là giao điểm của AB và CD
Xét ΔFAD có BC//AD
nên FB/BA=FC/CD
mà BA=CF
nên FB=FC
=>FA=FD
=>\(\widehat{BAD}=\widehat{D}=60^0\)
\(\widehat{ABC}=\widehat{DCB}=120^0\)
c: Xét ΔACD có
CE là đường trung tuyến
CE=AD/2
Do đó: ΔACD vuông tại C
Xét ΔABD có
BE là đường trung tuyến
BE=AD/2
Do đó: ΔABD vuông tại B
Bài 3:
Xét ΔCBD có CD=CB
nên ΔCBD cân tại C
Suy ra: \(\widehat{CDB}=\widehat{CBD}\)
mà \(\widehat{CDB}=\widehat{ADB}\)
nên \(\widehat{ADB}=\widehat{DBC}\)
mà hai góc này ở vị trí so le trong
nên AD//BC
hay ADCB là hình thang
Xét tứ giác ABCE có
là hình bình hành.
Lại có
là hình vuông cạnh a.
Bán kính đường tròn ngoại tiếp hình vuông ABCE là
R d = a 2 2
Sử dụng công thức tính nhanh bán kính mặt cầu ngoại tiếp chóp
S.ABCE là:
Chọn B.
Bài 4:
Xét ΔAED vuông tại E và ΔBFC vuông tại F có
AD=BC
góc D=góc C
Do đó: ΔAED=ΔBFC
=>DE=CF
Bài 3:
a: Xét ΔADC và ΔBCD có
AD=BC
AC=BD
DC chung
Do đó: ΔADC=ΔBCD
=>góc ACD=góc BDC
b: Ta co: góc ACD=góc BDC
=>góc EAB=góc EBA
=>ΔEAB cân tại E
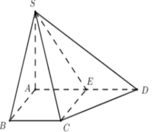
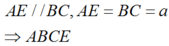
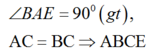
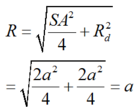
a) có ABCD là Hthang (gt)
=> BC // AD ( t/c Hthang)
mà E thuộc DA => BC // ED, BC // EA
AD = 2a (gt)
mà E là trung điểm DA => ED = EA = a
tứ giác ABCE có CB // EA (cmt)
CB = EA (=a)
=> ABCE là HBH ( vì là tứ giác có 2 cạnh đối vừa // vừa = nhau)
mà CB = BA (=a) => ABCE là H thoi ( vì là HBH có 2 cạnh kề = nhau)
=> CD = BE = a ( t/c Hthoi) (1)
CM tương tự ta được BCDE là Hthoi( vì là HBH có 2 cạnh kề = nhau)
=>CE = BA = a (t/c Hthoi) (2)
từ (1) và (2) => CE = BE = a
=>CE = BE = CB (= a)
=> CBE là tam giác đều => \(\widehat{CBE}=\widehat{CEB}=\widehat{ECB}=60^0\)
CDE là tam giác đều ( CD = DE = CE =a )
=> \(\widehat{CDE}=\widehat{DCE}=\widehat{CED}=60^0\)
tam giác EBA đều (BE = BA = EA =a)
=> \(\widehat{EBA}=\widehat{BAE}=\widehat{BEA}=60^0\)
có \(\widehat{C}=\widehat{DCE}+\widehat{BCE}=60^0+60^0=120^0\)
tương tự ta có \(\widehat{B}=120^0\)
vậy \(\widehat{A}=60^0,\widehat{D}=60^0,\widehat{C}=120^0,\widehat{D}=120^0\)
c) ABCE là Hthoi và CA là đường chéo
=> CA là tia phân giác của góc BAE ( t/c Hthoi)
=> \(\widehat{BAC}=\widehat{EAC}=30^0\)
tam giác CDA có \(\widehat{D}+\widehat{DCA}+\widehat{CAD}=180^0=>60^0+\widehat{DCA}+30^0=180^0\)
=> \(\widehat{DCA}=90^0\) =>tam giác CDA vuông tại C
cm tương tự ta được tam giác BDA vuông tại B
d) N là trung điểm của DE (gt)
M là trung điểm của EA (gt)
DE = EA = a
=>NM = a => BC = NM ( =a) (3)
có BC // AD ( T/C Hthang)
N,M thuộc AD => BC // NM (4)
từ (3) và (4) => BMNC là HBH ( vì là tứ giác có 2 cạnh đối vừa // vừa = nhau)
tam giác ABE đều (cmt) mà BM là đường trung tuyến
=>BM là tia phân giác của góc EBA
=> \(\widehat{EBM}=\widehat{ABM}=30^0\)
\(\Delta BMA\)có \(\widehat{BAM}+\widehat{BMA}+\widehat{MBA}=180^0=>60^0+\widehat{BMA}+30^0=180^0\)
=>\(\widehat{BMA}=90^0\)
hay \(\widehat{BMN}=90^0\)
HBH BMNC có \(\widehat{BMN}=90^0\)
=> BMNC là HCN ( vì là HBH có 1 góc vuông )
bạn có thể giúp mình giải câu b không Đào Thị Huyền