Giá trị biểu thức :
\(\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2+\left(\dfrac{1}{2}\right)^3+\left(\dfrac{1}{2}\right)^4+....+\left(\dfrac{1}{2}\right)^{20}\) Là :
A \(\dfrac{2^{20}-1}{2^{20}}\) B.\(\dfrac{1}{2}-\dfrac{1}{2^{20}}\)
C . 1 D . \(\dfrac{2^{20}-2}{2^{20}}\)
- Ghi cách giải nữa nha!




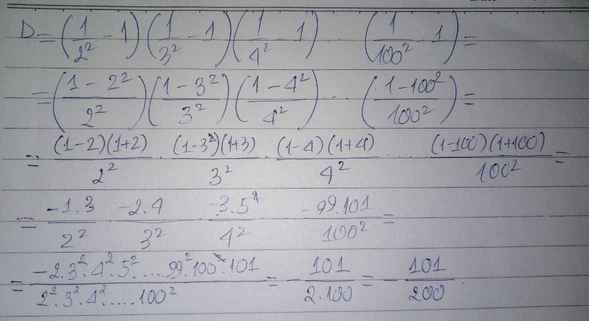
\(A=\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2+\left(\dfrac{1}{2}\right)^3+\left(\dfrac{1}{2}\right)^4+...+\left(\dfrac{1}{2}\right)^{20}\)
\(A=\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+\dfrac{1}{2^4}+...+\dfrac{1}{2^{20}}\)
\(2A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{19}}\)
\(2A-A=\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{99}}\right)-\left(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+\dfrac{1}{2^4}+...+\dfrac{1}{2^{20}}\right)\)
\(A=1-\dfrac{1}{2^{20}}=\dfrac{2^{20}-1}{2^{20}}\)
Chọn A