Cho đường tròn (O), dây cung CD, Qua O vẽ OH vuông góc với CD tại H, cắt tiếp tuyến tại C của đường tròn (O) tại M. Chứng minh MD là tiếp tuyến.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 1 2023
a: ΔOCD cân tại O
mà OH là đường cao
nên H là trung điểm của CD và OH là phân giác của góc COD
=>HC=HD=4cm
=>OH=3cm
OM=OC^2/OH=5^2/3=25/3(cm)
\(MC=\sqrt{\left(\dfrac{25}{3}\right)^2-5^2}=\dfrac{20}{3}\left(cm\right)\)
sin OCH=OH/OC=3/5
b: Xét ΔCOM và ΔDOM có
OC=OD
góc COM=góc DOM
OM chung
Do đo: ΔCOM=ΔDOM
=>góc DOM=90 độ
=>MD là tiếp tuyến của (O)
c: Xét tứ giác OCMD có
góc OCM+góc ODM=180 độ
nên OCMD là tứ giác nội tiếp
24 tháng 9 2021
Bn cần hình ko ạ?
Tam giác OCD có OC = OD (=R) => Tam giác OCD cân tại O.
=> Đường cao OH đồng thời là phân giác => góc COH = góc DOH.
Xét tam giác OCM và tam giác ODM có:
OC = OD (=R)
OM chung;
góc COH = góc DOH (cmt);
=> Tam giác OCM = tam giác ODM (c.g.c)
=> Góc OCM = góc ODM (2 góc tương ứng).
Mà góc OCM = 90 độ (MC là tiếp tuyến của (O) => MC vuông góc với OC tại C).
=> góc ODM = 90 độ
=> MD vuông góc với bán kính OD của (O) tại điểm D thuộc (O).
Vậy MD là tiếp tuyến của (O) tại D.
CM
25 tháng 3 2018
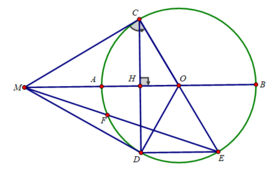
a) Xét tam giác COD cân tại O có OH là đường cao
⇒ OH cũng là tia phân giác ⇒ ∠(COM) = ∠(MOD)
Xét ΔMCO và ΔMOD có:
CO = OD
∠(COM) = ∠(MOD)
MO là cạnh chung
⇒ ΔMCO = ΔMOD (c.g.c)
⇒ ∠(MCO) = ∠(MDO)
∠(MCO) = 90 0 nên ∠(MDO) = 90 0
⇒ MD là tiếp tuyến của (O)
Xét ΔOCD có OC=OD
nen ΔOCD cân tại O
mà OM là đường cao
nên OM là phân giác của góc COD
Xét ΔMCO và ΔMDO có
OC=OD
\(\widehat{MOC}=\widehat{MOD}\)
OM chung
Do đó: ΔMCO=ΔMDO
Suy ra: \(\widehat{MCO}=\widehat{MDO}=90^0\)
hay MD là tiếp tuyến của (O)