Tính tổng sau A=1+5+52+53+...+52015
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=2+2^2+...+2^{20}\)
\(2A=2^2+2^3+...+2^{21}\)
\(2A-A=2^2+2^3+...+2^{21}-2-2^2-...-2^{20}\)
\(A=2^{21}-2\)
___________
\(B=5+5^2+...+5^{50}\)
\(5B=5^2+5^3+...+5^{51}\)
\(5B-B=5^2+5^3+...+5^{51}-5-5^2-...-5^{50}\)
\(4B=5^{51}-5\)
\(B=\dfrac{5^{51}-5}{4}\)
___________
\(C=1+3+3^2+...+3^{100}\)
\(3C=3+3^2+...+3^{101}\)
\(3C-C=3+3^2+...+3^{101}-1-3-3^2-...-3^{100}\)
\(2C=3^{101}-1\)
\(C=\dfrac{3^{101}-1}{2}\)

A = 5 + 5² + 5³ + ... + 5²⁰²³
⇒ 5A = 5² + 5³ + 5⁴ + ... + 5²⁰²⁴
⇒ 4A = 5A - A
= (5² + 5³ + 5⁴ + ... + 5²⁰²⁴) - (5 + 5² + 5³ + ... + 5²⁰²³)
= 5²⁰²⁴ - 5
⇒ A = (5²⁰²⁴ - 5)/4
A = 5 + 5² + 5³ + ... + 5²⁰²³
⇒ 5A = 5² + 5³ + 5⁴ + ... + 5²⁰²⁴
⇒ 4A = 5A - A
= (5² + 5³ + 5⁴ + ... + 5²⁰²⁴) - (5 + 5² + 5³ + ... + 5²⁰²³)
= 5²⁰²⁴ - 5
⇒ A = (5²⁰²⁴ - 5)/4

Đề bài thiếu yêu cầu cụ thể em nhé. em cập nhật lại câu hỏi để được sự hỗ trợ tốt nhất cho tài khoản olm vip

a.
$S=1+2+2^2+2^3+...+2^{2017}$
$2S=2+2^2+2^3+2^4+...+2^{2018}$
$\Rightarrow 2S-S=(2+2^2+2^3+2^4+...+2^{2018}) - (1+2+2^2+2^3+...+2^{2017})$
$\Rightarrow S=2^{2018}-1$
b.
$S=3+3^2+3^3+...+3^{2017}$
$3S=3^2+3^3+3^4+...+3^{2018}$
$\Rightarrow 3S-S=(3^2+3^3+3^4+...+3^{2018})-(3+3^2+3^3+...+3^{2017})$
$\Rightarrow 2S=3^{2018}-3$
$\Rightarrow S=\frac{3^{2018}-3}{2}$
Câu c, d bạn làm tương tự a,b.
c. Nhân S với 4. Kết quả: $S=\frac{4^{2018}-4}{3}$
d. Nhân S với 5. Kết quả: $S=\frac{5^{2018}-5}{4}$

Ta có:\(\frac{1}{51}+\frac{1}{52}+...+\frac{1}{100}=\left(1+\frac{1}{2}+...+\frac{1}{100}\right)-\left(1+\frac{1}{2}+...+\frac{1}{50}\right)=\left(1+\frac{1}{2}+...+\frac{1}{100}\right)-2.\left(\frac{1}{2}+\frac{1}{4}+...+\frac{1}{100}\right)\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{99}-\frac{1}{100}=1-\frac{1}{100}=\frac{99}{100}\)
@Ác Mộng ở đoạn cuối tự nhiên bỏ mất số 2 luôn, giải sai rồi kìa

5A=5+5^2+...+5^2023
=>4A=5^2023-1
=>\(A=\dfrac{5^{2023}-1}{4}\)
\(2B-A=\dfrac{5^{2023}}{4}-\dfrac{5^{2023}-1}{4}=\dfrac{1}{4}\)
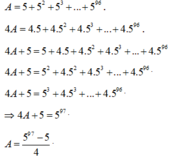
=> 5A = 5 + 52 + ... + 52016
=> 5A - A = 52016 - 5
=> 4A = 52016 - 5
=> A = \(\frac{5^{2016}-5}{4}\)