Cho \(\Delta\)ABC , vẽ đường thẳng M sao cho \(\widehat{BAM}\) bằng và so le trong với \(\widehat{B}\), vẽ đường thẳng N sao cho \(\widehat{CAN}\)bằng và so le trong với \(\widehat{C}\).Chứng tỏ rằng M,A,N thẳng hàng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
25 tháng 12 2017
Ta có B A M ^ = B ^ suy ra AM // BC (vì có cặp góc so le trong bằng nhau).
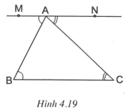
C A N ^ = C ^ suy ra AN // BC (vì có cặp góc so le trong bằng nhau).
Theo tiên đề Ơ-clít qua điểm A chỉ có một đường thẳng song song với BC, do đó ba điểm M, A, N thẳng hàng
18 tháng 9 2023
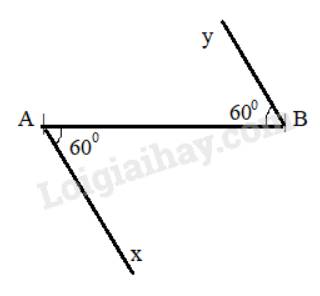
Hai đường thẳng chứa hai tia Ax và By có song song với nhau. Vì \(\widehat {xAB} = \widehat {yBA}( = 60^\circ )\), mà hai góc này ở vị trí so le trong nên Ax // By (Dấu hiệu nhận biết 2 đường thẳng song song).
26 tháng 5 2022
a: \(\widehat{ABC}=180^0-80^0-50^0=50^0\)
\(\widehat{BAD}=180^0-80^0=100^0\)
\(\Leftrightarrow\widehat{DAM}=\dfrac{100^0}{2}=50^0=\widehat{EDA}\)
mà hai góc này ở vị trí so le trong
nên DE//AM
b: Ta có: \(\widehat{BAD}=100^0\)
nên \(\widehat{MAB}=\dfrac{100^0}{2}=50^0=\widehat{ABC}\)
mà hai góc này ở vị trí so le trong
nên AM//BC
c: \(\widehat{ABC}=\widehat{ACB}\left(=50^0\right)\)
20 tháng 11 2020
a) Xét tam giác ABC có Góc A + góc B+ góc C = 180 độ ( định í tổng 3 góc trong một tam giác
Suy ra góc C = 40 độ
b) Xét tam giác vuông BHC có góc BAC + góc ABH = 90 độ => góc ABH = 50 độ
Xét tam giác vuông HBC có góc BCA+ góc CBH = 90 độ=> góc CAH = 50 độ
Vì góc ABH = góc CAH
nên BH là phân giác của góc ABH)
c) vì Ax song song với BH
Cy song song với BH
nên Ax vuông góc với AC, Cy vuông góc với AC
Ta có góc BCy = góc BCA + góc ACy= 40 độ + 90 độ = 130 độ
Góc xAB + góc ABC + góc BCy = 90 độ + 60 độ + 130 độ = 280 độ
Ta có: \(\widehat{BAM}=\widehat{B}\)
mà hai góc này ở vị trí so le trong
nên AM//BC
Ta có: \(\widehat{CAN}=\widehat{C}\)
mà hai góc này ở vị trí so le trong
nên AN//BC
Ta có: AM//BC
AN//BC
AM,AN có điểm chung là A
Do đó: A,M,N thẳng hàng