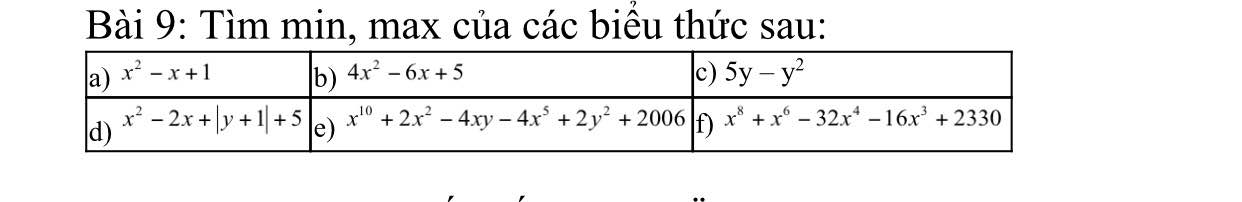Giải hộ em câu này theo phương pháp quy đổi với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NQ
1
30 tháng 7 2021
Ta có : \(\frac{A}{B}\ge\frac{x}{4}+5\Leftrightarrow\sqrt{x}+4\ge\frac{x}{4}+5\)
\(\Leftrightarrow\frac{4\sqrt{x}+16}{4}-\frac{x}{4}-\frac{20}{4}\ge0\Leftrightarrow\frac{4\sqrt{x}-x-4}{4}\ge0\)
\(\Rightarrow-x+4\sqrt{x}-4\ge0\Leftrightarrow x-4\sqrt{x}+4\le0\)vì 4 > 0
\(\Leftrightarrow\left(\sqrt{x}-2\right)^2\le0\Leftrightarrow x\le4\)
Kết hợp với đk vậy \(0\le x\le4;x\ne1\)
2 tháng 2 2023
Bạn ko đưa ngữ liệu, đưa ngang như v ai hiểu gì đâu
Bạn học sách mới mà.
17 tháng 3 2022
Tự do kinh doanh nhưng không kinh doanh, buôn bán chất cấm, thứ ảnh hưởng đến sức khoẻ và tính mạng người dùng,...Kinh doanh làm sao để phát triển được bền lâu mà vẫn giữ nguyên phẩm giá, lương tâm của một người tốt. Không có các hành vi buôn bán gây ảnh hưởng đến xã hội, mất trật tự xã hội vì như vậy là hành vi sai trái, và nhà nước cũng nghiêm cấm việc đó với các hộ kinh doanh...
NN
17 tháng 3 2022
Theo mình thấy , nếu như tự do kinh doanh thì cần phải tuân theo quy định của pháp luật và sự quản lý của nhà nước , như vậy mới đảm bảo được mặt hàng kinh doanh không bị vi phạm pháp luật . Vậy nên , khi buôn bán tự do kinh doanh mà nhập hàng uy tín, không phải hàng chất cấm là điều tốt , nên làm như vậy
A
1
12 tháng 12 2021
a: Xét tứ giác OBAC có
\(\widehat{OBA}+\widehat{OCA}=180^0\)
Do đó: OBAC là tứ giác nội tiếp
TA
11 tháng 8 2021
B, Đồ thị y thì nhìn vào dáng điệu, đồ thị y' thì chú ý trục hoành
20 tháng 1 2022
a: \(\text{Δ}=1-4m\)
Để phương trình vô nghiệm thì -4m+1<0
=>m>1/4
Để phương trình có nghiệm kép thì -4m+1=0
hay m=1/4
Để phương trình có vô số nghiệm thì -4m+1>0
hay m<1/4
b: \(\text{Δ}=9-4\cdot1\cdot\left(-m\right)=4m+9\)
Để phương trình vô nghiệm thì 4m+9<0
hay m<-9/4
Để phương trình có nghiệm kép thì 4m+9=0
hay m=-9/4
Để phương trình có 2 nghiệm phân biệt thì 4m+9>0
hay m>-9/4
28 tháng 8 2021
a: Ta có: \(x^2-x+1\)
\(=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)
d: Ta có: \(x^2-2x+\left|y+1\right|+5\)
\(=\left(x-1\right)^2+\left|y+1\right|+4\ge4\forall x,y\)
Dấu '=' xảy ra khi x=1 và y=-1
12 tháng 12 2021
\(b,\Leftrightarrow\left\{{}\begin{matrix}m+2=1\\m\ne2\end{matrix}\right.\Leftrightarrow m=-1\\ c,\text{PT giao Ox: }y=0\Leftrightarrow\left(m+2\right)x-m=0\\ \text{Thay }x=2\Leftrightarrow2m+4-m=0\\ \Leftrightarrow m=-4\\ d,\text{PT giao Ox và Oy: }\\ y=0\Leftrightarrow x=\dfrac{m}{m+2}\Leftrightarrow A\left(\dfrac{m}{m+2};0\right)\Leftrightarrow OA=\left|\dfrac{m}{m+2}\right|\\ x=0\Leftrightarrow y=-m\Leftrightarrow B\left(0;-m\right)\Leftrightarrow OB=\left|m\right|\\ \Delta OAB\text{ cân }\Leftrightarrow OA=OB\Leftrightarrow\left|\dfrac{m}{m+2}\right|=\left|m\right|\\ \Leftrightarrow\left[{}\begin{matrix}\dfrac{m}{m+2}=m\\\dfrac{m}{m+2}=-m\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m\left(m+1\right)=0\\m\left(m+3\right)=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=0\\m=-1\\m=-3\end{matrix}\right.\)