Cho tam giác ABC trung tuyến AM trọng tâm G.Chứng minh:
SAMB = SAMC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
3 tháng 9 2019
Kẻ đường cao AH
Ta có: SAMB = 0.5.BM.AH
SAMC = 0.5.CM.AH
Mà BM = CM (gt)
Þ SAMB = SAMC (ĐPCM)
CM
1 tháng 5 2019
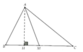
Kẻ đường cao AH.
Ta có:
Mà BM = CM (vì AM là trung tuyến)
⇒ SAMB = SAMC (đpcm).
10 tháng 3 2023
Đề có sai không bạn , nếu `Delta ABC` là tam giác thường thôi thì không cm đc đâu ạ
DA
18 tháng 5 2021
Xét tam giác ABC, ta có:
Đtt AM (gt)
G là trọng tâm (gt)
=> G thuộc AM ( t/c)
=> 3 điểm A,G,M thẳng hàng (đpcm)
S
4 tháng 3 2023
câu 2 :
a) có phải là chứng minh AM ⊥ BC không
xét ΔAMB và ΔAMC, ta có :
AB = AC (2 cạnh bên của ΔABC cân tại A)
MB = MC (AM là đường trung tuyến của cạnh BC)
AM là cạnh chung
=> ΔAMB = ΔAMC (c.c.c)
=> \(\widehat{AMB}=\widehat{AMC}\) (2 cạnh tương ứng)
mà \(\widehat{AMB}+\widehat{AMC}=180^O\) (kề bù)
\(\Rightarrow\widehat{AMB}=\widehat{AMC}=\dfrac{180^O}{2}=90^O\)
=> AM ⊥ BC
\(\dfrac{ab}{ae}\)+\(\dfrac{ac}{af}\)=3
AF ở đâu vậy