2sin3x=cosx
phương trình đẳng cấp bậc 2 ạ
cos3x+sin3x=sinx-cosx
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\Leftrightarrow cos3x+\sqrt{3}sin3x=\sqrt{3}cosx+sinx\)
\(\Leftrightarrow\dfrac{1}{2}cos3x+\dfrac{\sqrt{3}}{2}sin3x=\dfrac{\sqrt{3}}{2}cosx+\dfrac{1}{2}sinx\)
\(\Leftrightarrow cos\left(3x-\dfrac{\pi}{3}\right)=cos\left(x-\dfrac{\pi}{6}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-\dfrac{\pi}{3}=x-\dfrac{\pi}{6}+k2\pi\\3x-\dfrac{\pi}{3}=\dfrac{\pi}{6}-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{12}+k\pi\\x=\dfrac{\pi}{8}+\dfrac{k\pi}{2}\end{matrix}\right.\)

ĐKXĐ: ...
\(sin3x-cos3x+sinx+cosx=\dfrac{sin3x-cos3x+sinx+cosx}{\left(sin3x+cosx\right)\left(cos3x-sinx\right)}\)
\(\Rightarrow\left[{}\begin{matrix}sin3x-cos3x+sinx+cosx=0\left(1\right)\\\left(sin3x+cosx\right)\left(cos3x-sinx\right)=1\left(2\right)\end{matrix}\right.\)
(1) \(\Leftrightarrow3sinx-4sin^3x-4cos^3x+3cosx+sinx+cosx=0\)
\(\Leftrightarrow sinx+cosx+sin^3x+cos^3x=0\)
\(\Leftrightarrow sinx+cosx+\left(sinx+cosx\right)\left(1-sinx.cosx\right)=0\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(2-sinx.cosx\right)=0\)
\(\Leftrightarrow sinx+cosx=0\) (loại)
(2) \(\Leftrightarrow sin3x.cos3x-sinx.cosx-sin3x.sinx+cos3x.cosx=1\)
\(\Leftrightarrow\dfrac{1}{2}sin6x-\dfrac{1}{2}sin2x+cos4x=1\)
\(\Leftrightarrow\dfrac{1}{2}\left(3sin2x-4sin^32x\right)-\dfrac{1}{2}sin2x+1-2sin^22x=1\)
\(\Leftrightarrow sin2x-2sin^32x-2sin^22x=0\)
\(\Leftrightarrow-sin2x\left(2sin^22x+2sin2x-1\right)=0\)
\(\Leftrightarrow...\)

\(\Leftrightarrow\dfrac{1}{2}sinx+\dfrac{\sqrt{3}}{2}cosx=sin3x\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{3}\right)=sin3x\)
\(\Leftrightarrow\left[{}\begin{matrix}3x=x+\dfrac{\pi}{3}+k2\pi\\3x=\dfrac{2\pi}{3}-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=\dfrac{\pi}{6}+\dfrac{k\pi}{2}\end{matrix}\right.\)
\(\Leftrightarrow x=\dfrac{\pi}{6}+\dfrac{k\pi}{2}\)

\(\Leftrightarrow sin3x.cosx+cos3x.sinx-2\left(sin^23x+cos^23x\right)+cos3x=0\)
\(\Leftrightarrow sin4x+cos3x-2=0\)
Do \(\left\{{}\begin{matrix}sin4x\le1\\cos3x\le1\end{matrix}\right.\) \(\Rightarrow sin4x+cos3x-2\le0\)
Dấu "=" xảy ra khi và chỉ khi: \(\left\{{}\begin{matrix}sin4x=1\\cos3x=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x=\frac{\pi}{2}+k2\pi\\3x=n2\pi\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=\frac{\pi}{8}+\frac{k\pi}{2}\\x=\frac{n2\pi}{3}\end{matrix}\right.\)
Biểu diễn trên đường tròn lượng giác thì 2 tập nghiệm này ko có điểm chung
Vậy pt vô nghiệm

2.1
a.
\(\Leftrightarrow sinx-cosx=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\sqrt{2}sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=\dfrac{\pi}{6}+k2\pi\\x-\dfrac{\pi}{4}=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5\pi}{12}+k2\pi\\x=\dfrac{13\pi}{12}+k2\pi\end{matrix}\right.\)
b.
\(cosx-\sqrt{3}sinx=1\)
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{3}=\dfrac{\pi}{3}+k2\pi\\x+\dfrac{\pi}{3}=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)

Chọn D
Ta sẽ biến đổi phương trình thành dạng tích
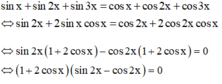
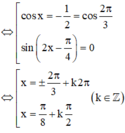
Chú ý: có thể dùng 4 đáp án thay vào phương trình để kiểm tra đâu là nghiệm

Chọn A
Ta có: - sin 3 x + cos 3 x = sin x – cos x
⇔ ( c os x- sin x) . ( c os 2 x + c osx. sin x+sin 2 x ) + ( c os x - sin x) = 0 ⇔ ( c os x- sin x) . ( 1 + c osx. sin x ) + ( c os x - sin x) = 0 ⇔ ( c osx - sin x ). (1+ c os x. sinx + 1 ) = 0 ⇔ ( c osx - sin x ). (2+ sin 2 x 2 ) = 0 ⇔ cosx - sinx = 0 sin 2 x 2 = − 2
cosx - sin x =0 ⇔ 2 cos x + π 4 = 0 ⇔ cos x + π 4 = 0 ⇔ x + π 4 = π 2 + k π ⇔ x = π 4 + k π
sin 2 x 2 = − 2 ⇔ sin 2 x = − 4 < − 1 n ê n l o ạ i
Vậy nghiệm của phương trình đã cho là: x = π 4 + k π
2sin3x = cosx (sin2x + cos2x)
⇔ 2sin3x - sin2x cosx - cos3x = 0
+ Xét cosx = 0 ........
+ Xét cosx khác 0 rồi chia cho cos3x rồi đưa về phương trình bậc 3 của tanx
sin3x + cos3x = sinx - cosx
Nhân cos2x + sin2x là thành câu trên