Cho hàm số y=(m-2)x+5 Tìm m để khoảng cách từ gốc tọa độ O đến (d) bằng 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
A
1
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 8 2021
Với \(m=2\Rightarrow y=5\) khoảng cách từ O đến d bằng 5 (ktm)
Với \(m\ne2\):
Gọi A là giao điểm của d với Ox \(\Rightarrow A\left(-\dfrac{5}{m-2};0\right)\Rightarrow OA=\dfrac{5}{\left|m-2\right|}\)
Gọi B là giao điểm của d với Oy \(\Rightarrow B\left(0;5\right)\Rightarrow OB=5\)
Trong tam giác vuông OAB, hạ \(OH\perp AB\Rightarrow\) OH là khoảng cách từ O đến d \(\Rightarrow OH=3\)
Áp dụng hệ thức lượng:
\(\dfrac{1}{OA^2}+\dfrac{1}{OB^2}=\dfrac{1}{OH^2}\Leftrightarrow\dfrac{\left(m-2\right)^2}{25}+\dfrac{1}{25}=\dfrac{1}{9}\)
\(\Leftrightarrow\left(m-2\right)^2=\dfrac{16}{9}\Rightarrow\left[{}\begin{matrix}m-2=\dfrac{4}{3}\\m-2=-\dfrac{4}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m=\dfrac{10}{3}\\m=\dfrac{2}{3}\end{matrix}\right.\)
CM
19 tháng 1 2019
Chọn C
Ta có y ' = 3 x 2 - 6 m x + 3 ( m 2 - 1 )
Hàm số (1) có cực trị thì PT y ' = 0 có 2 nghiệm phân biệt
⇔ x 2 - 2 m x + m 2 - 1 = 0 có 2 nhiệm phân biệt
Khi đó, điểm cực đại A ( m - 1 ; 2 - 2 m ) và điểm cực tiểu B ( m + 1 ; - 2 m )
Ta có O A = 2 O B ⇔ m 2 + 6 m + 1 = 0
5 tháng 12 2023
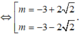
a: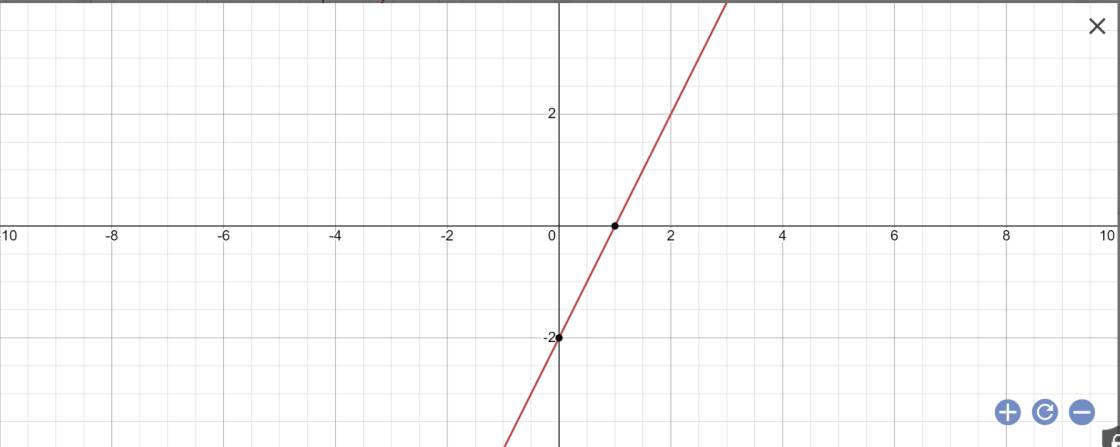 
b: Để (d)//(d') thì \(\left\{{}\begin{matrix}m+1=2\\6< >-2\left(đúng\right)\end{matrix}\right.\)
=>m+1=2
=>m=1
c:
(d'): y=(m+1)x+6
=>(m+1)x-y+6=0
Khoảng cách từ O đến (d') là:
\(d\left(O;\left(d'\right)\right)=\dfrac{\left|0\cdot\left(m+1\right)+0\cdot\left(-1\right)+6\right|}{\sqrt{\left(m+1\right)^2+\left(-1\right)^2}}\)
\(=\dfrac{6}{\sqrt{\left(m+1\right)^2+1}}\)
Để \(d\left(O;\left(d'\right)\right)=3\sqrt{2}\) thì \(\dfrac{6}{\sqrt{\left(m+1\right)^2+1}}=3\sqrt{2}\)
=>\(\sqrt{\left(m+1\right)^2+1}=\sqrt{2}\)
=>\(\left(m+1\right)^2+1=2\)
=>\(\left(m+1\right)^2=1\)
=>\(\left[{}\begin{matrix}m+1=1\\m+1=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=0\\m=-2\end{matrix}\right.\)
25 tháng 1 2020
Bạn viết sai rồi, đường thẳng y-mx+2 =0 hay y=mx+2 vậy bạn?
AH
Akai Haruma
Giáo viên
30 tháng 7 2021
Lời giải:
$y'=3x^2-6mx+3(m^2-1)=0$
$\Leftrightarrow x^2-2mx+m^2-1=0$
$\Leftrightarrow x=m+1$ hoặc $x=m-1$
Với $x=m+1$ thì $y=-2m-2$. Ta có điểm cực trị $(m+1, -2m-2)$
Với $x=m-1$ thì $y=2-2m$. Ta có điểm cực trị $m-1, 2-2m$
$f''(m+1)=6>0$ nên $A(m+1, -2m-2)$ là điểm cực tiểu
$f''(m-1)=-6< 0$ nên $B(m-1,2-2m)$ là điểm cực đại
$BO=\sqrt{2}AO$
$\Leftrightarrow BO^2=2AO^2$
$\Leftrightarrow (m-1)^2+(2-2m)^2=2(m+1)^2+2(-2m-2)^2$
$\Leftrightarrow m=-3\pm 2\sqrt{2}$