(2x-1)2 = 64
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 7 2016
a, (2x-3)3 = -64
=> (2x-3)3 = -43
=> 2x-3=-4
=> 2x = -1
=> x = -1 : 2
=> x = -1/2
b, (2x-3)2 =25
=> (2x-3)2 =5^2
=> 2x-3 = 5
=> 2x = 8
=> x = 4
c, (3x-4)2 =36
=> (3x-4)2 =62
=> 3x-4 = 6
=> 3x = 10
=> x = 3.(3)
d, 2x+1 = 64
=> 2x+1 = 26
=> x+1 = 6
=> x = 5
H9
HT.Phong (9A5)
CTVHS
12 tháng 8 2023
\(\left(x-3\right)=\left(3-x\right)^2\)
\(\Leftrightarrow x-3=\left(x-3\right)^2\)
\(\Leftrightarrow\left(x-3\right)-\left(x-3\right)^2=0\)
\(\Leftrightarrow\left(x-3\right)\left[1-\left(x-3\right)\right]=0\)
\(\Leftrightarrow\left(x-3\right)\left(4-x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\4-x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=4\end{matrix}\right.\)
___________
\(x^3+\dfrac{3}{2}x^2+\dfrac{3}{4}x+\dfrac{1}{8}=\dfrac{1}{64}\)
\(\Leftrightarrow x^3+3\cdot\dfrac{1}{2}\cdot x^2+3\cdot\left(\dfrac{1}{2}\right)^2\cdot x+\left(\dfrac{1}{2}\right)^3=\dfrac{1}{64}\)
\(\Leftrightarrow\left(x+\dfrac{1}{2}\right)^3=\left(\dfrac{1}{4}\right)^3\)
\(\Leftrightarrow x+\dfrac{1}{2}=\dfrac{1}{4}\)
\(\Leftrightarrow x=\dfrac{1}{4}-\dfrac{1}{2}\)
\(\Leftrightarrow x=-\dfrac{1}{4}\)
GS
0
VT
1
NV
25 tháng 9 2019
a, 2x-1 = 64
=> 2x-1 = 26
=> x - 1 = 6
=> x = 6 + 1
=> x = 7
b, 32x-10 = 81
=> 32x-10 = 34
=> 2x - 10 = 4
=> 2x = 14
=> x = 7
c, 22x+3 = 1024
=> 22x+3 = 210
=> 2x + 3 = 10
=> 2x = 7
=> x = \(\frac{7}{2}\)
H9
HT.Phong (9A5)
CTVHS
11 tháng 7 2023
\(M=\left(7-2x\right)\left(4x^2+14x+49\right)-\left(64-8x^3\right)\)
\(M=\left(7-2x\right)\left[\left(2x\right)^2+2x\cdot7+7^2\right]-\left(64-8x^3\right)\)
\(M=\left[7^3-\left(2x\right)^3\right]-\left(64-8x^3\right)\)
\(M=343-8x^3-64+8x^3\)
\(M=279\)
Vậy M có giá trị 279 với mọi x
\(P=\left(2x-1\right)\left(4x^2-2x+1\right)-\left(1-2x\right)\left(1+2x+4x^2\right)\)
\(P=8x^3-4x^2+2x-4x^2+2x-1-1+8x^3\)
\(P=16x^3-8x^2+4x-2\)
Thay \(x=10\) vào P ta có:
\(P=16\cdot10^3-8\cdot10^2+4\cdot10-2=15238\)
Vậy P có giá trị 15238 tại x=10
10 tháng 7 2023
a: M=343-8x^3-64+8x^3=279
b: P=8x^3-4x^2+2x-4x^2+2x-1-1+8x^3
=16x^3-8x^2+4x-2
=16*10^3-8*10^2+4*10-2=15238
23 tháng 10 2016
\(\left(2x-1\right)^6=64^2\)
\(\Leftrightarrow\left(2x-1\right)^6=4^6\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}2x-1=4\\2x-1=-4\end{array}\right.\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x=\frac{5}{2}\\x=-\frac{3}{2}\end{array}\right.\)
23 tháng 10 2016
\(\left(2x-1\right)^6=64^2\)
\(\Rightarrow\left(2x-1\right)^6=4^6\)
\(\Rightarrow2x-1=\pm4\)
+) \(2x-1=4\Rightarrow x=\frac{5}{2}\)
+) \(2x-1=-4\Rightarrow x=\frac{-3}{2}\)
Vậy \(x=\frac{5}{2}\) hoặc \(x=\frac{-3}{2}\)
MV
8 tháng 8 2017
\(\dfrac{2x}{15}+\dfrac{2x}{35}+\dfrac{2x}{63}+...+\dfrac{2x}{195}=\dfrac{4}{5}\\ x\cdot\left(\dfrac{2}{15}+\dfrac{2}{35}+\dfrac{2}{63}+...+\dfrac{2}{195}\right)=\dfrac{4}{5}\\ x\cdot\left(\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+\dfrac{2}{7\cdot9}+...+\dfrac{2}{13\cdot15}\right)=\dfrac{4}{5}\\ x\cdot\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+...+\dfrac{1}{13}-\dfrac{1}{15}\right)=\dfrac{4}{5}\\ x\cdot\left(\dfrac{1}{3}-\dfrac{1}{15}\right)=\dfrac{4}{5}\\ x\cdot\dfrac{4}{15}=\dfrac{4}{5}\\ x=\dfrac{4}{5}:\dfrac{4}{15}\\ x=3\)
Gọi \(D=\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{8}-\dfrac{1}{16}+\dfrac{1}{32}-\dfrac{1}{64}\)
\(2D=1-\dfrac{1}{2}+\dfrac{1}{4}-\dfrac{1}{8}+\dfrac{1}{16}-\dfrac{1}{32}\\ 2D+D=\left(1-\dfrac{1}{2}+\dfrac{1}{4}-\dfrac{1}{8}+\dfrac{1}{16}-\dfrac{1}{32}\right)+\left(\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{8}-\dfrac{1}{16}+\dfrac{1}{32}-\dfrac{1}{64}\right)\\ 3D=1-\dfrac{1}{2}+\dfrac{1}{4}-\dfrac{1}{8}+\dfrac{1}{16}-\dfrac{1}{32}+\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{8}-\dfrac{1}{16}+\dfrac{1}{32}-\dfrac{1}{64}\\ 3D=1-\dfrac{1}{64}< 1\\ \Rightarrow D=\dfrac{1-\dfrac{1}{64}}{3}< \dfrac{1}{3}\)
Vậy \(\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{8}-\dfrac{1}{16}+\dfrac{1}{32}-\dfrac{1}{64}< \dfrac{1}{3}\)
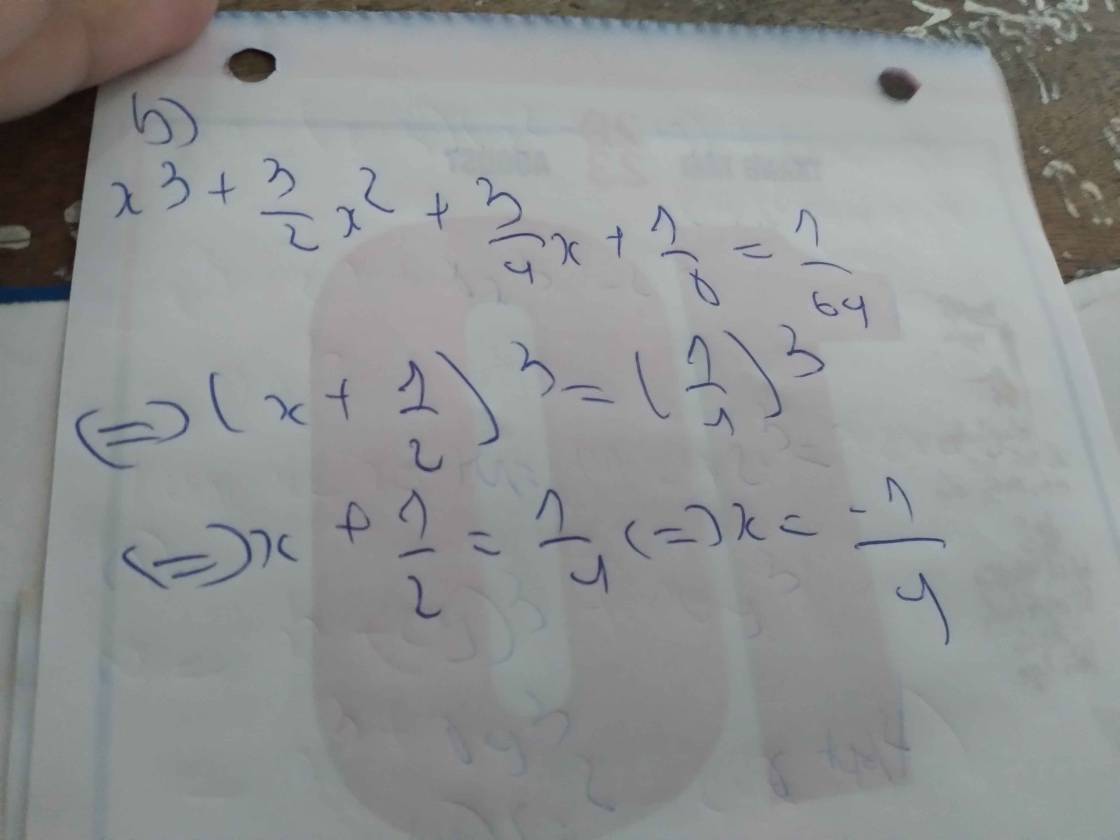
\(\left(2x-1\right)^2=64\)
\(\Rightarrow\left[{}\begin{matrix}2x-1=8\\2x-1=-8\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{9}{2}\\x=-\dfrac{7}{2}\end{matrix}\right.\)
Vậy..............
Ta có: (2x - 1)2 = 64
\(\Rightarrow\left[{}\begin{matrix}2x-1=8\\2x-1=-8\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}2x=9\\2x=-7\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{9}{2}\\x=-\dfrac{7}{2}\end{matrix}\right.\)
Vậy \(x_1=\dfrac{9}{2};x_2=-\dfrac{7}{2}\)