cho hình chóp sabc có sa=sb=sc=2a, tam giác abc đều cạnh a. tính thể tích khối chóp sab
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(AC=\sqrt{BC^2-AB^2}=\dfrac{a\sqrt{3}}{4}\)
Gọi H là hình chiếu vuông góc của S lên đáy
Do \(SA=SB=SC\Rightarrow HA=HB=HC\Rightarrow H\) là tâm đường tròn ngoại tiếp ABC
Mà ABC vuông tại A \(\Rightarrow H\) là trung điểm BC
\(\Rightarrow BH=\dfrac{1}{2}BC=\dfrac{a}{2}\)
\(\Rightarrow SH=\sqrt{SB^2-BH^2}=\dfrac{a\sqrt{15}}{2}\)
\(V=\dfrac{1}{3}SH.\dfrac{1}{2}AB.AC=\dfrac{1}{3}.\dfrac{a\sqrt{15}}{2}.\dfrac{1}{2}.\dfrac{a}{2}.\dfrac{a\sqrt{3}}{4}=\dfrac{a^3\sqrt{5}}{32}\)

Đáp án A
Gọi H là trung điểm AB. Ta có 2 tam giác SAB và ABC đều và bằng nhau nên SH = CH= a 3 . Mà S Δ A B C = a 2 3 ⇒ V S . A B C = 1 3 a 2 3 . a 3 = a 3

Đáp án là A
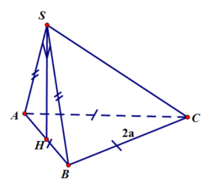
![]()
![]()
![]()
Ta có :
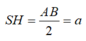
( Do SAB là tam giác vuông cân tại S cạnh huyền AB=2a)
Diện tích tam giác ABC là

Vậy thể tích khối chóp SABC là:
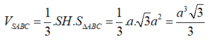

Đáp án B
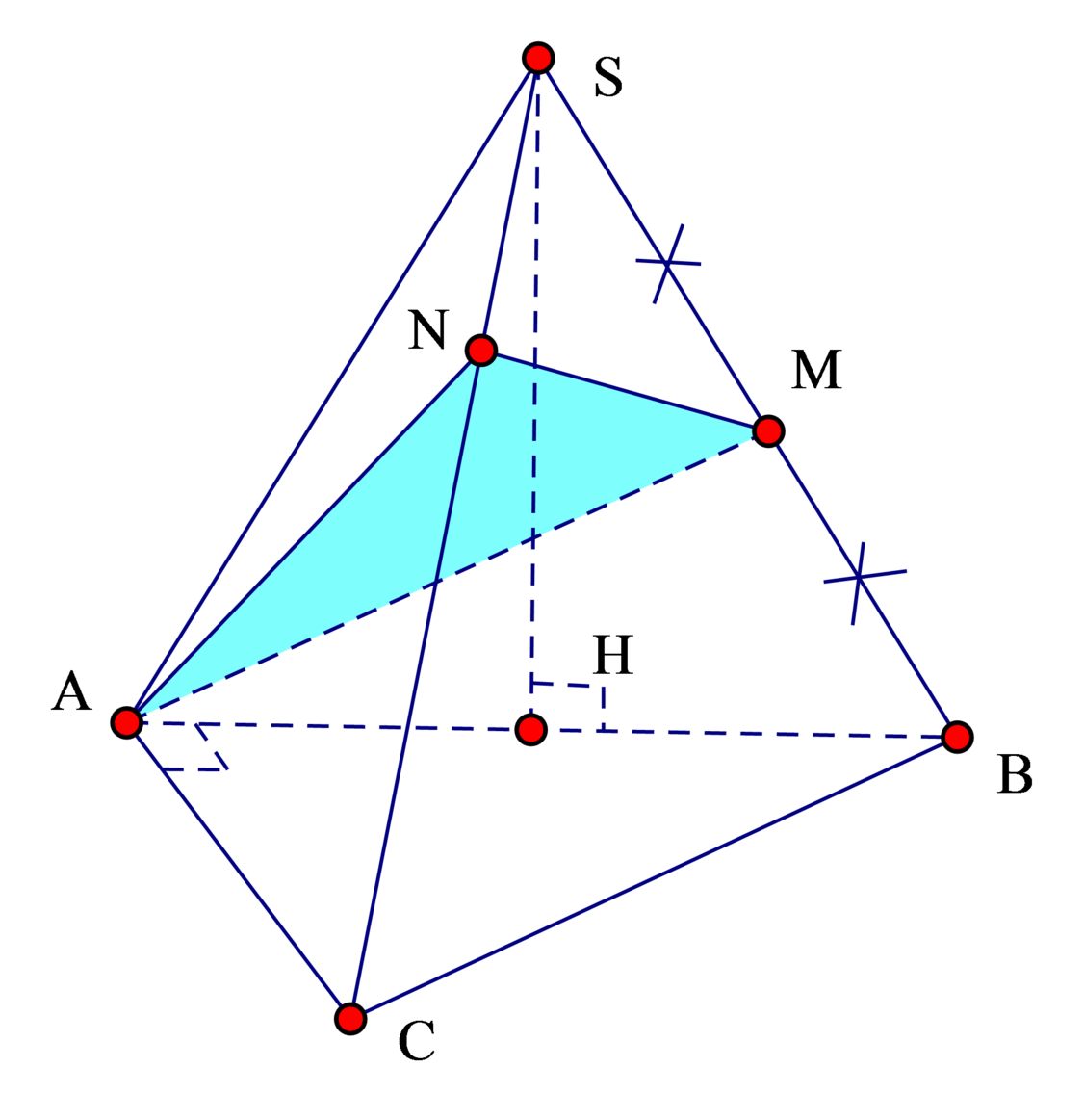
Kẻ đường cao SH trong Δ S A B ⇒ A H ⊥ A B C .
Δ S A B đều ⇒ A H = 2. a 3 2 = a 3
Diện tích tam giác: A B C = 1 2 . 2 a 2 = 2 a 2
⇒ V S . A B C = 1 3 S H . d t A B C = 1 3 a 3 .2 a 2 = 2 a 3 3 3
Ta có: V S . A M N V S . A B C = S M S B . S N S C = 1 2 . 1 3 = 1 6
⇒ V S . A M N = V S . A B C 6 = 2 a 3 3 3.6 = a 3 3 9

Phương pháp:
Tính thể tích V S . A B C
Tính thể tích V S . A M N theo công thức tỉ lệ thể tích
Tính thể tích V A . B C M N và suy ra kết luận
Cách giải:
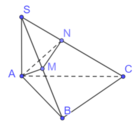
Xét tam giác SAB và SAC là các tam giác vuông tại A có hai cạnh góc vuông là a và 2a nên
![]()
Tam giác SAB vuông tại có đường cao AM
Khi đó ![]()
Tương tự ![]()
Lại có ![]()
Mặt khác 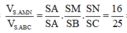
![]()
Do đó ![]()
![]()
Chọn C.


Gọi H là tâm đáy \(\Rightarrow SH\perp\left(ABC\right)\)
Ta có: \(AH=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\)
Áp dụng định lý Pitago:
\(SH=\sqrt{SA^2-AH^2}=\dfrac{a\sqrt{33}}{3}\)
\(V=\dfrac{1}{3}SH.S_{ABC}=\dfrac{1}{3}.\dfrac{a\sqrt{33}}{3}.\dfrac{a^2\sqrt{3}}{4}=\dfrac{a^3\sqrt{11}}{12}\)