Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(AC=\sqrt{BC^2-AB^2}=\dfrac{a\sqrt{3}}{4}\)
Gọi H là hình chiếu vuông góc của S lên đáy
Do \(SA=SB=SC\Rightarrow HA=HB=HC\Rightarrow H\) là tâm đường tròn ngoại tiếp ABC
Mà ABC vuông tại A \(\Rightarrow H\) là trung điểm BC
\(\Rightarrow BH=\dfrac{1}{2}BC=\dfrac{a}{2}\)
\(\Rightarrow SH=\sqrt{SB^2-BH^2}=\dfrac{a\sqrt{15}}{2}\)
\(V=\dfrac{1}{3}SH.\dfrac{1}{2}AB.AC=\dfrac{1}{3}.\dfrac{a\sqrt{15}}{2}.\dfrac{1}{2}.\dfrac{a}{2}.\dfrac{a\sqrt{3}}{4}=\dfrac{a^3\sqrt{5}}{32}\)

Đáp án là A
![]()
![]()
![]()
Ta có :
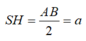
( Do SAB là tam giác vuông cân tại S cạnh huyền AB=2a)
Diện tích tam giác ABC là

Vậy thể tích khối chóp SABC là:

Phương pháp:
Tính thể tích V S . A B C
Tính thể tích V S . A M N theo công thức tỉ lệ thể tích
Tính thể tích V A . B C M N và suy ra kết luận
Cách giải:
Xét tam giác SAB và SAC là các tam giác vuông tại A có hai cạnh góc vuông là a và 2a nên
![]()
Tam giác SAB vuông tại có đường cao AM
Khi đó ![]()
Tương tự ![]()
Lại có ![]()
Mặt khác 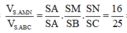
![]()
Do đó ![]()
![]()
Chọn C.

Đáp án C
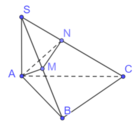
Gọi M, N lần lượt là trung điểm của AB và CD
Tam giác SAB cân tại S suy ra S M ⊥ A B
⇒ S M ⊥ d , với d = ( S A B ) ∩ ( S C D )
Vì ( S A B ) ⊥ ( S C D ) suy ra S M ⊥ ( S C D )
![]()
Kẻ S H ⊥ M N ⇒ S H ⊥ ( A B C D )
Ta có S ∆ S A B + S ∆ S C D = 7 a 2 10
![]()
⇒ S M + S N = 7 a 5
Tam giác SMN vuông tại S nên S M 2 + S N 2 = M N 2 = a 2
Giải hệ S M + S N = 7 a 5 S M 2 + S N 2 = a 2
![]()
![]()
Vậy thể tích khối chóp V S . A B C D = 1 3 . S A B C D . S H = 4 a 3 25

Đáp án D
Gọi H là trung điểm của BC.
Do tam giác ABC vuông cân tại A nên H là tâm đường tròn ngoại tiếp tam giác ABC.
Mặt khác do SA=SB=SC nên S thuộc trục đường tròn ngoại tiếp ABC
⇒ S H ⊥ A B C A H = B C 2 = a , S H = S A 2 - A H 2 = a A B = A C = B C 2 a 2
Thể tích khối chóp là
V = 1 3 . S H . 1 2 . A B . A C = a 3 3
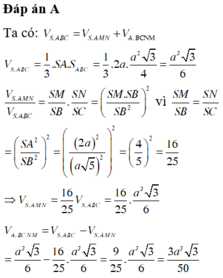
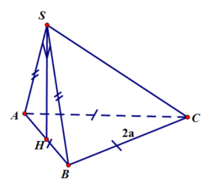
Gọi H là tâm đáy \(\Rightarrow SH\perp\left(ABC\right)\)
Ta có: \(AH=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\)
Áp dụng định lý Pitago:
\(SH=\sqrt{SA^2-AH^2}=\dfrac{a\sqrt{33}}{3}\)
\(V=\dfrac{1}{3}SH.S_{ABC}=\dfrac{1}{3}.\dfrac{a\sqrt{33}}{3}.\dfrac{a^2\sqrt{3}}{4}=\dfrac{a^3\sqrt{11}}{12}\)