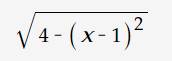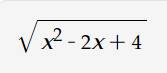K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 8 2021
- p lon nhat khi x = 7 , p nho nhat khi x = 6
- p lon nhat = 2554 , p nho nhat = 2014
dung khong ta ?
7 tháng 1 2020
các bạn trả lời nhanh giúp mình nhé, ngày mai cô kiểm tra rồi
H9
HT.Phong (9A5)
CTVHS
30 tháng 8 2023
Ta có:
\(A=\sqrt{4\sqrt{x}-x}\) (ĐK: \(16\ge x\ge0\))
Mà: \(\sqrt{4\sqrt{x}-x}\ge0\forall x\)
Dấu "=" xảy ra:
\(4\sqrt{x}-x=0\)
\(\Leftrightarrow4\sqrt{x}-\left(\sqrt{x}\right)^2=0\)
\(\Leftrightarrow\sqrt{x}\left(4-\sqrt{x}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=0\\4-\sqrt{x}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=16\end{matrix}\right.\)
Vậy: \(A_{min}=0\) khi \(\left[{}\begin{matrix}x=0\\x=16\end{matrix}\right.\)
VT
1
16 tháng 8 2023
ĐKXĐ: 4-(x-1)^2>=0
=>(x-1)^2<=4
=>-2<=x-1<=2
=>-1<=x<=3
\(\left(x-1\right)^2>=0\)
=>-(x-1)^2<=0
=>\(-\left(x-1\right)^2+4< =4\)
=>\(\sqrt{-\left(x-1\right)^2+4}< =2\)
Dấu = xảy ra khi x=1
\(\sqrt{4-\left(x-1\right)^2}>=0\forall x\) thỏa mãn ĐKXĐ
Dấu = xảy ra khi 4-(x-1)^2=0
=>(2-x+1)(2+x-1)=0
=>(3-x)(1+x)=0
=>x=3 hoặc x=-1
VT
1
16 tháng 8 2023
`\sqrt{x^2 - 2x + 4}`
`=\sqrt{(x-1)^2 + 3}`
Do `\sqrt{(x-1)^2 + 3} >=0`
`(x-1)^{2} >=0`
`=>(x-1)^{2} + 3 >=3AAx`
`=>\sqrt{(x-1)^2 + 3} >= \sqrt{3}AAx`
Dấu "=" xảy ra `<=>x-1=0`
`<=>x=1`
Vậy `min` của biểu thức là `\sqrt{3} <=>x=1`
VA
2
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 4 2022
\(\left\{{}\begin{matrix}a^2\ge0\\a^4+a^2+1>0\end{matrix}\right.\) ;\(\forall a\Rightarrow P=\dfrac{a^2}{a^4+a^2+1}\ge0\)
\(P_{min}=0\) khi \(a=0\)
\(P=\dfrac{3a^2}{3\left(a^4+a^2+1\right)}=\dfrac{a^4+a^2+1-\left(a^4-2a^2+1\right)}{3\left(a^4+a^2+1\right)}=\dfrac{1}{3}-\dfrac{\left(a^2-1\right)^2}{3\left(a^4+a^2+1\right)}\le\dfrac{1}{3}\)
\(P_{max}=\dfrac{1}{3}\) khi \(a^2=1\Rightarrow a=\pm1\)
XO
16 tháng 4 2022
Ta có \(3P=\dfrac{3a^2}{a^4+a^2+1}=\dfrac{-a^4+2a^2-1+a^4+a^2+1}{a^4+a^2+1}=1-\dfrac{\left(a^2-1\right)^2}{a^4+a^2+1}\le1\)\(\Rightarrow P\le\dfrac{1}{3}\)
Dấu "=" xảy ra <=> a2 - 1 = 0 <=> a = \(\pm1\)
Vậy Max P = 1/3 khi a = \(\pm1\)
+) Dễ thấy \(P=\dfrac{a^2}{a^4+a^2+1}\ge0\) ("=" khi a = 0)
Vậy \(0\le P\le\dfrac{1}{3}\)
4 tháng 7 2020
Bài làm:
#Tìm Max của biểu thức:
\(A=\frac{3-4x}{x^2+1}=\frac{4\left(x^2+1\right)-\left(4x^2+4x+1\right)}{x^2+1}=4-\frac{\left(2x+1\right)^2}{x^2+1}\)
Mà \(\hept{\begin{cases}\left(2x+1\right)^2\ge0\\x^2+1>0\end{cases}\left(\forall x\right)\Rightarrow}-\frac{\left(2x+1\right)^2}{x^2+1}\le0\left(\forall x\right)\)
\(\Rightarrow A\le4\left(\forall x\right)\)
Dấu "=" xảy ra khi: \(\left(2x+1\right)^2=0\Rightarrow x=-\frac{1}{2}\)
Vậy \(Max\left(A\right)=4\Leftrightarrow x=-\frac{1}{2}\)
#Tìm Max và Min của B:
Tìm Min
\(B=\frac{2x}{x^2+1}=\frac{\left(x^2+2x+1\right)-\left(x^2+1\right)}{x^2+1}=\frac{\left(x+1\right)^2}{x^2+1}-1\)
Mà \(\hept{\begin{cases}\left(x+1\right)^2\ge0\\x^2+1>0\end{cases}\left(\forall x\right)\Rightarrow}\frac{\left(x+1\right)^2}{x^2+1}\ge0\left(\forall x\right)\)
\(\Rightarrow B\ge-1\left(\forall x\right)\)
Dấu "=" xảy ra khi: \(\left(x+1\right)^2\ge0\Rightarrow x=-1\)
Vậy \(Min\left(B\right)=-1\Leftrightarrow x=-1\)
Tìm Max
\(B=\frac{2x}{x^2+1}=\frac{x^2+1-\left(x^2-2x+1\right)}{x^2+1}=1-\frac{\left(x-1\right)^2}{x^2+1}\)
Mà \(\hept{\begin{cases}\left(x-1\right)^2\ge0\\x^2+1>0\end{cases}}\left(\forall x\right)\Rightarrow-\frac{\left(x-1\right)^2}{x^2+1}\le0\left(\forall x\right)\)
\(\Rightarrow B\le1\left(\forall x\right)\)
Dấu "=" xảy ra khi: \(\left(x-1\right)^2=0\Rightarrow x=1\)
Vậy \(Max\left(B\right)=1\Leftrightarrow x=1\)
Sao dạo này nhìu bạn đăng mấy câu như vậy lên thế nhỉ?