Tìm giá trị nhỏ nhất của biểu thức A = \(3x^2-\dfrac{9x}{4}+\dfrac{3}{16x}\) với x dương.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 7 2021
a.
\(A=x^2+\dfrac{2021}{x}=x^2+\dfrac{2021}{2x}+\dfrac{2021}{2x}\ge3\sqrt[3]{\dfrac{2021^2}{4x^2}}=3\sqrt[3]{\dfrac{2021^2}{4}}\)
Dấu "=" xảy ra khi \(x=\sqrt[3]{\dfrac{2021}{3}}\)
b.
\(B=4\left(x-1\right)+\dfrac{25}{x-1}+4\ge2\sqrt{\dfrac{100\left(x-1\right)}{x-1}}+4=24\)
Dấu "=" xảy ra khi \(x=\dfrac{7}{2}\)
c.
\(C=3x+\dfrac{16}{x^3}=x+x+x+\dfrac{16}{x^3}\ge4\sqrt[4]{\dfrac{16x^3}{x^3}}=8\)
\(A_{min}=8\) khi \(x=2\)
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 7 2021
d.
\(D=x+\dfrac{1}{x}=\left(\dfrac{x}{4}+\dfrac{1}{x}\right)+\dfrac{3}{4}.x\ge2\sqrt{\dfrac{x}{4x}}+\dfrac{3}{4}.2=\dfrac{5}{2}\)
Dấu "=" xảy ra khi \(x=2\)
e.
\(E=\dfrac{9\left(x-2\right)+18}{2-x}+\dfrac{2}{x}=2\left(\dfrac{1}{x}+\dfrac{9}{2-x}\right)-9\ge\dfrac{2.\left(1+3\right)^2}{x+2-x}-9=7\)
\(E_{min}=7\) khi \(x=\dfrac{1}{5}\)
f.
\(F=\dfrac{3}{1-x}+\dfrac{4}{x}\ge\dfrac{\left(\sqrt{3}+2\right)^2}{1-x+x}=7+4\sqrt{3}\)
Dấu "=" xảy ra khi \(x=4-2\sqrt{3}\)
22 tháng 1
a: Để \(\dfrac{3x-2}{4}\) không nhỏ hơn \(\dfrac{3x+3}{6}\) thì \(\dfrac{3x-2}{4}>=\dfrac{3x+3}{6}\)
=>\(\dfrac{6\left(3x-2\right)}{24}>=\dfrac{4\left(3x+3\right)}{24}\)
=>18x-12>=12x+12
=>6x>=24
=>x>=4
b: Để \(\left(x+1\right)^2\) nhỏ hơn \(\left(x-1\right)^2\) thì \(\left(x+1\right)^2< \left(x-1\right)^2\)
=>\(x^2+2x+1< x^2-2x+1\)
=>4x<0
=>x<0
c: Để \(\dfrac{2x-3}{35}+\dfrac{x\left(x-2\right)}{7}\) không lớn hơn \(\dfrac{x^2}{7}-\dfrac{2x-3}{5}\) thì
\(\dfrac{2x-3}{35}+\dfrac{x\left(x-2\right)}{7}< =\dfrac{x^2}{7}-\dfrac{2x-3}{5}\)
=>\(\dfrac{2x-3+5x\left(x-2\right)}{35}< =\dfrac{5x^2-7\cdot\left(2x-3\right)}{35}\)
=>\(2x-3+5x^2-10x< =5x^2-14x+21\)
=>-8x-3<=-14x+21
=>6x<=24
=>x<=4
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 12 2020
Chắc đề bài là \(Q=\dfrac{3}{9x^2+6xy+y^2}+\dfrac{3}{3x^2+6xy+2y^2}\)
Từ giả thiết ta có:
\(2x^3+2xy^2+xy^2+y^3=2\left(x^2+y^2\right)\)
\(\Leftrightarrow2x\left(x^2+y^2\right)+y\left(x^2+y^2\right)=2\left(x^2+y^2\right)\)
\(\Leftrightarrow2x+y=2\)
Do đó:
\(Q=3\left(\dfrac{1}{9x^2+6xy+y^2}+\dfrac{1}{3x^2+6xy+2y^2}\right)\)
\(Q\ge\dfrac{3.4}{12x^2+12xy+3y^2}=\dfrac{4}{\left(2x+y\right)^2}=1\)
\(Q_{min}=1\) khi \(\left\{{}\begin{matrix}2x+y=2\\9x^2+6xy+y^2=3x^2+6xy+2y^2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\sqrt{6}-2\\y=6-2\sqrt{6}\end{matrix}\right.\)
XO
21 tháng 8 2023
ĐKXĐ : \(x\ne0;x\ne\pm1\)
a) Bạn ghi lại rõ đề.
b) \(B=\dfrac{x-1}{x+1}+\dfrac{3x-x^2}{x^2-1}=\dfrac{x-1}{x+1}+\dfrac{3x-x^2}{\left(x-1\right).\left(x+1\right)}\)
\(=\dfrac{\left(x-1\right)^2+3x-x^2}{\left(x-1\right).\left(x+1\right)}=\dfrac{x+1}{\left(x-1\right).\left(x+1\right)}=\dfrac{1}{x-1}\)
c) \(P=A.B=\dfrac{x^2+x-2}{x.\left(x-1\right)}=\dfrac{\left(x-1\right).\left(x+2\right)}{x\left(x-1\right)}=\dfrac{x+2}{x}=1+\dfrac{2}{x}\)
Không tồn tại Min P \(\forall x\inℝ\)
8 tháng 9 2021
\(P\left(x\right)=\dfrac{4x^4+16x^3+56x^2+80x+356}{x^2+2x+5}\\ P\left(x\right)=\dfrac{4x^2\left(x^2+2x+5\right)+8x\left(x^2+2x+5\right)+20\left(x^2+2x+5\right)+256}{x^2+2x+5}\\ P\left(x\right)=4\left(x^2+2x+5\right)+\dfrac{256}{x^2+2x+5}\\ \ge2\sqrt{\dfrac{4\left(x^2+2x+5\right)\cdot256}{x^2+2x+5}}=2\sqrt{1024}=64\left(BĐTcosi\right)\)
Dấu \("="\Leftrightarrow4\left(x^2+2x+5\right)=\dfrac{256}{x^2+2x+5}\)
\(\Leftrightarrow x^2+2x+5=8\Leftrightarrow x^2+2x-3=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\)
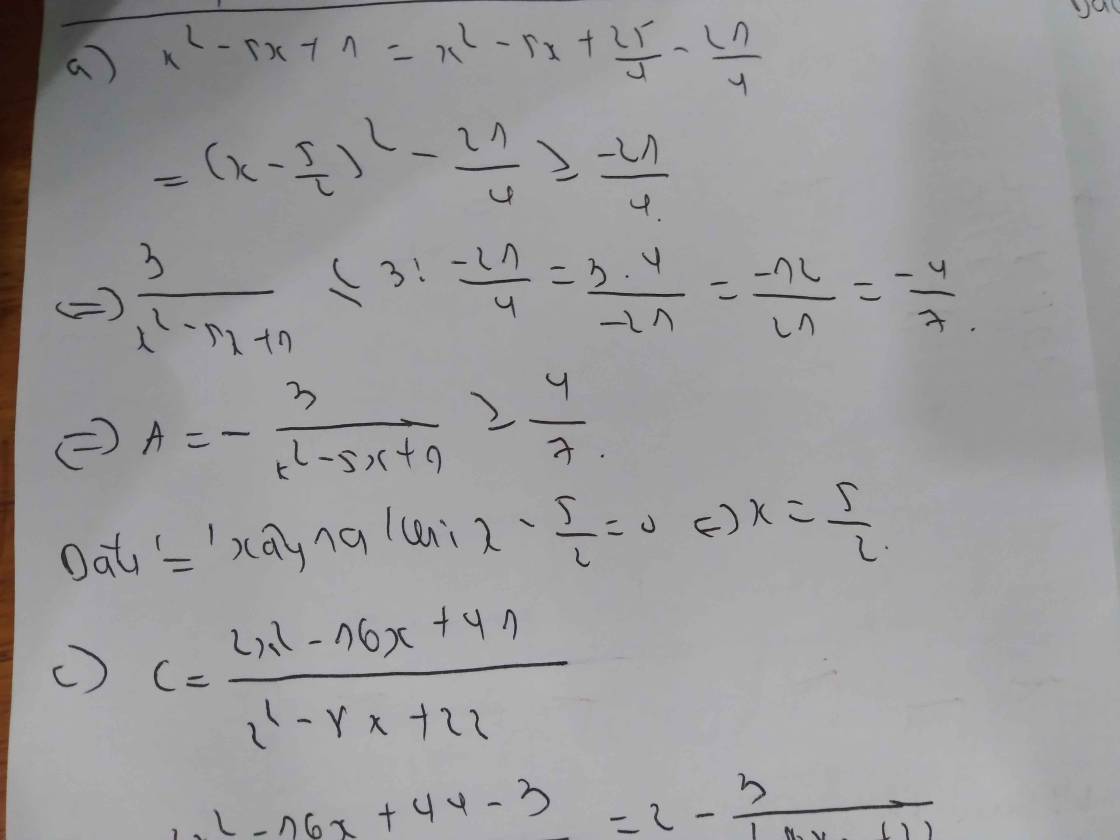
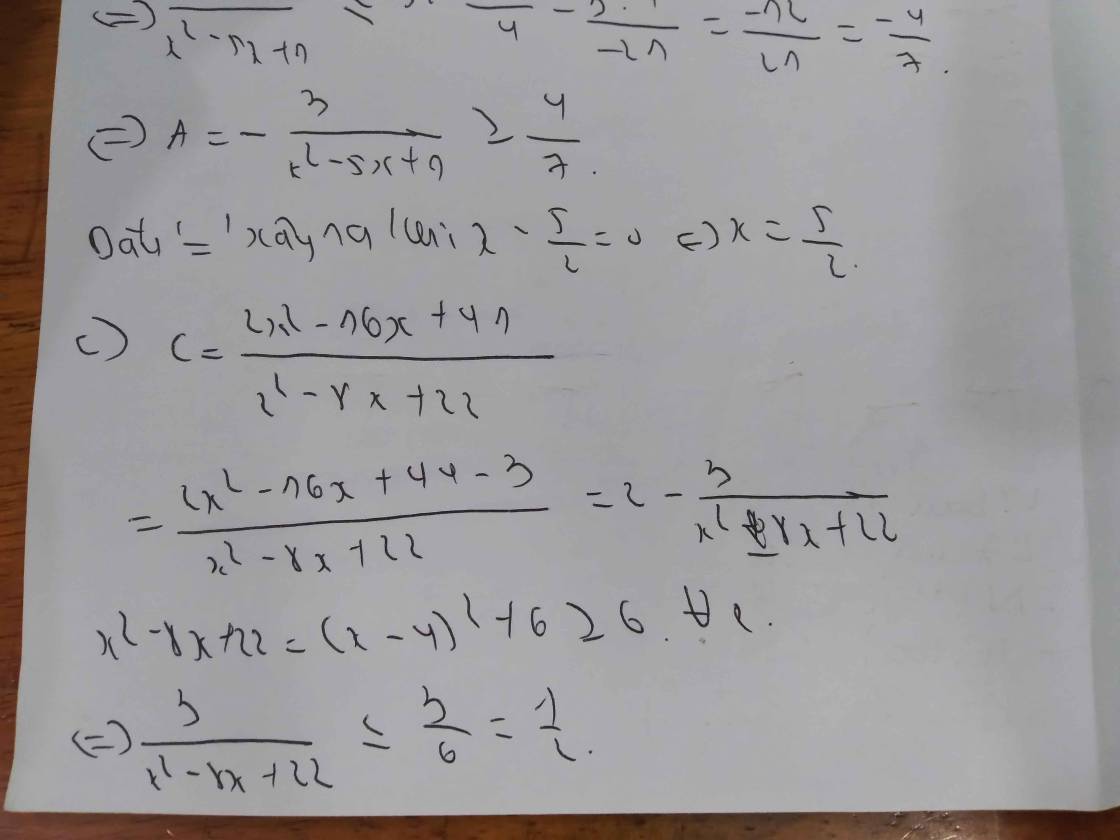
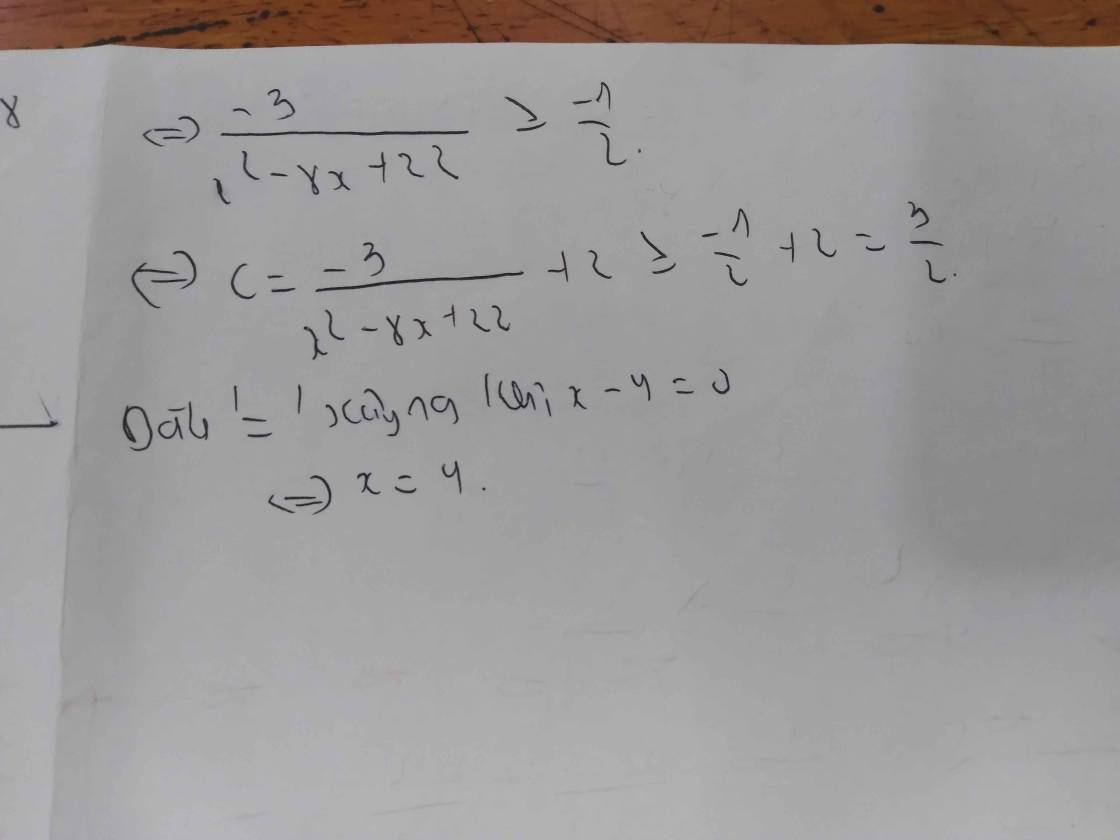
\(A=3x^2-\dfrac{9x}{4}+\dfrac{3}{16x}=\left(3x^2-3x+\dfrac{3}{4}\right)+\left(\dfrac{3}{16x}+\dfrac{3x}{4}\right)-\dfrac{3}{4}\)
\(=3\left(x-\dfrac{1}{2}\right)^2+\left(\dfrac{3}{16x}+\dfrac{3x}{4}\right)-\dfrac{3}{4}\)
\(\ge2\sqrt{\dfrac{3}{16}.\dfrac{3}{4}}-\dfrac{3}{4}=0\)
Vậy GTNN là A = 0 khi \(x=\dfrac{1}{2}\)