Cho đường tròn tâm O đường kính AB. Gọi M là một điểm nẳm trên đường tròn, tính số đo góc AMB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


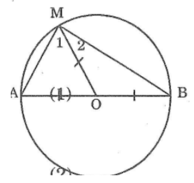
Nối OM, ta có:
OA = OM (bán kính đường tròn tâm O)
Nên ΔOAM cân tại O
⇒∠A =∠M1(tính chất tam giác cân)(1)
OM = OB (bán kính đường tròn tâm O)
Suy ra: ΔOBM cân tại O
⇒∠B =∠M2(tính chất tam giác cân) (2)
Trong ΔAMB ta có:
∠A + ∠AMB + ∠B = 180º (tổng ba góc trong tam giác)
⇒∠A +∠B +∠M1+∠M2 =180 (3)
Từ (1), (2) và (3) suy ra: 2(∠M1 + ∠M2)=180o
Vậy: ∠M1+∠M2=90o hay ∠(AMB) =90o

vì M thuộc đường tròn tâm C đường kính AB nen ta có CA=CM=CB=R
vậy tam giác CAM cân tại C và tam giác CBM cân tại C
vì tam giác CAM cân tại C nên ta có góc CMA = góc CAM = (180-góc ACM):2
vì tam giác CBM cân tại C nên ta có góc CBM= góc CMB= (180-góc BCM):2
ta lại có góc AMB= góc AMC + góc BMC=\(\frac{180-gócACM}{2}\frac{ }{ }\)+\(\frac{180-gócBCM}{2}\frac{ }{ }\)=\(\frac{180+180-gócACM-gócBCM}{2}\frac{ }{ }\)=\(\frac{360-gócACB}{2}\frac{ }{ }\)=\(\frac{360-180}{2}\frac{ }{ }\)=90 độ

Giải thích các bước giải:
MO là t.p.g. của AMBˆAMB^
⇒AMOˆ=BMOˆ=AMBˆ2=450⇒AMO^=BMO^=AMB^2=450
⇒ΔAMO−và−ΔBMO⇒ΔAMO−và−ΔBMO vuông cân
=> OA = AM = MB = BO
=> OAMB là h.thoi có AMBˆ=900AMB^=900
=> OAMB là h.v.
b)
PMPQ=MP+MQ+PQPMPQ=MP+MQ+PQ
=(MP+PC)+(MQ+QC)=(MP+PC)+(MQ+QC)
=(MP+PA)+(MQ+QB)=(MP+PA)+(MQ+QB)
=MA+MB=MA+MB
=2OA=2OA
=2R=2R
c)
OP−là−t.p.g.−của−AOCˆOP−là−t.p.g.−của−AOC^
⇒COPˆ=12AOCˆ⇒COP^=12AOC^ (1)
OQ−là−t.p.g.−của−BOCˆOQ−là−t.p.g.−của−BOC^
⇒COQˆ=12BOCˆ⇒COQ^=12BOC^ (2)
Cộng theo vế của (1) và (2), ta có:
COPˆ+COQˆ=12(AOCˆ+BOCˆ)=12AOBˆCOP^+COQ^=12(AOC^+BOC^)=12AOB^
⇒POQˆ=450
Giải thích các bước giải:
MO là t.p.g. của AMBˆAMB^
⇒AMOˆ=BMOˆ=AMBˆ2=450⇒AMO^=BMO^=AMB^2=450
⇒ΔAMO−và−ΔBMO⇒ΔAMO−và−ΔBMO vuông cân
=> OA = AM = MB = BO
=> OAMB là h.thoi có AMBˆ=900AMB^=900
=> OAMB là h.v.
b)
PMPQ=MP+MQ+PQPMPQ=MP+MQ+PQ
=(MP+PC)+(MQ+QC)=(MP+PC)+(MQ+QC)
=(MP+PA)+(MQ+QB)=(MP+PA)+(MQ+QB)
=MA+MB=MA+MB
=2OA=2OA
=2R=2R
c)
OP−là−t.p.g.−của−AOCˆOP−là−t.p.g.−của−AOC^
⇒COPˆ=12AOCˆ⇒COP^=12AOC^ (1)
OQ−là−t.p.g.−của−BOCˆOQ−là−t.p.g.−của−BOC^
⇒COQˆ=12BOCˆ⇒COQ^=12BOC^ (2)
Cộng theo vế của (1) và (2), ta có:
COPˆ+COQˆ=12(AOCˆ+BOCˆ)=12AOBˆCOP^+COQ^=12(AOC^+BOC^)=12AOB^
⇒POQˆ=450vv

Bài 7:
a: Xét ΔOAM vuông tại A có
\(\cos\widehat{AOM}=\dfrac{OA}{OM}=\dfrac{1}{2}\)
nên \(\widehat{AOM}=60^0\)
b: Xét tứ giác OAMB có
\(\widehat{OAM}+\widehat{OBM}=180^0\)
Do đó: OAMB là tứ giác nội tiếp
Suy ra: \(\widehat{AOB}=180^0-36^0=144^0\)

a: Đề bài này chưa đủ dữ kiện để tính góc OAC nha bạn
ΔOAC cân tại O
mà OD là đường trung tuyến
nên OD\(\perp\)AC và OD là phân giác của góc AOC
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>AC\(\perp\)CB
mà OD\(\perp\)AC
nên OD//CB
b: Xét ΔOAE và ΔOCE có
OA=OC
\(\widehat{AOE}=\widehat{COE}\)
OE chung
Do đó: ΔOAE=ΔOCE
=>\(\widehat{OAE}=\widehat{OCE}=90^0\)
=>EC là tiếp tuyến của (O)
(h.141)\(\Delta AOM\) cân \(\Rightarrow\)\(\widehat{A}=\widehat{M1}\)
\(\Delta BOM\) cân \(\Rightarrow\)\(\widehat{B}=\widehat{M2}\)
Suy ra \(\widehat{M1}+\widehat{M2}=\widehat{A}+\widehat{B}\)do đó
\(\widehat{AMB}=\widehat{A}+\widehat{B}\).Ta lại có:
\(\widehat{AMB}+\widehat{A}+\widehat{B}=180^0\) nên
\(\widehat{AMB}=90^0\)
(h.141)ΔAOM=>A^=M1^
ΔBOMΔBOM cân ⇒B^=M2^
Suy ra ˆM1+ˆM2=ˆA+ˆBdo đó
ˆAMB=ˆA+ˆB.Ta lại có:
ˆAMB+ˆA+ˆB=180o nên
ˆAMB=90o