Trong mặt phẳng phức cho hai điểm M,N lần lượt biểu diễn các số phức z, w=\(\dfrac{1}{\overline{z}}\) (z#0) . Giả sử điểm M di động trên đường tròn (C): \(^{\left(X+1\right)^2}\)+\(\left(Y-1\right)^2\)=2
thì tập hợp điểm N là:
A. Đường thẳng 2x-2y+1=0.
B. Đường thẳng 2x+2y+1=0.
C. Đường tròn tâm (2;2) bán kính bằng 1.
D. Đường tròn tâm (2;-2) bán kính bằng 1


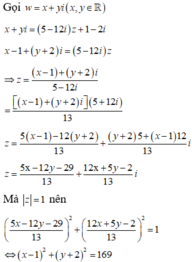




Lời giải:
Nếu gọi \(z=a+bi\Rightarrow w=\frac{1}{\overline{z}}=\frac{z}{|z|^2}=\frac{a+bi}{a^2+b^2}\)
Điểm \(M\) di động trên $(C)$ nên \((a+1)^2+(b-1)^2=2\)
\(\Rightarrow a^2+b^2=2b-2a\)
Từ đây ta có:
\(\frac{2a}{a^2+b^2}=\frac{2a}{2b-2a};\frac{2b}{a^2+b^2}=\frac{2b}{2b-2a}\Rightarrow \frac{2a}{a^2+b^2}-\frac{2b}{a^2+b^2}=-1\)
Tương đương với việc tập hợp các điểm biểu diễn số phức \(w\) nằm trên đường thẳng \(2x-2y+1=0\)
Đáp án A.