Cho điểm A nằm trong góc vuông xOy. Gọi M, N lần lượt là chân đường vuông góc kẻ từ A đến Ox, Oy. Biết AM = AN = 3cm. Khi đó :
(A) OM = ON > 3cm (B) OM = ON < 3cm
(C) OM = ON = 3cm (D) \(OM\ne ON\)
Hãy chọn phương án đúng ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

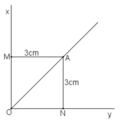
+) Vì A nằm trong góc xOy và cách đều Ox, Oy (AM = AN = 3cm) nên điểm A nằm trên tia phân giác của góc xOy.
Suy ra: OA là tia phân giác của góc xOy.
Suy ra:
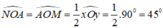
+) Tam giác AOM vuông tại M có góc 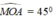 nên
nên
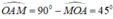
Suy ra; tam giác OAM vuông cân tại M nên OM = MA = 3cm.
+) Chứng minh tương tự ta có tam giác OAN vuông cân tại N nên :
ON = NA = 3cm
Vậy OM = ON = 3cm
Chọn C.

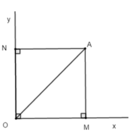
Vì A nằm trong góc xOy và cách đều hai tia Ox và Oy nên A nằm trên tia phân giác của góc xOy hay OA là tia phân giác của góc xOy
⇒ N O A ^ = M O A ^ = 1 2 x O y ^ = 1 2 .90 ° = 45 °
Tam giác MOA vuông tại M có M O A ^ = 45 °
Suy ra tam giác MAO vuông cân tại M nên MO = MA = 4 cm
Chứng minh tương tự ta cũng có NOA vuông cân tại N nên NO = NA = 4 cm
Vậy OM = ON = 4 cm.
Chọn đáp án C

a
Do Ox là đường trung trực của MA nên OM=OA ( 1 )
Do Oy là đường trung trực của NA nên ON=OA ( 2 )
Từ ( 1 );( 2 ) suy ra đpcm
b
Từ ( 1 ) suy ra \(\widehat{mOx}=\widehat{xOA}=\frac{1}{2}\widehat{MOA}\left(3\right)\)
Từ ( 2 ) suy ra \(\widehat{AOy}=\widehat{yON}=\frac{\widehat{AON}}{2}\left(4\right)\)
Từ ( 3 );( 4 ) suy ra \(\frac{1}{2}\left(\widehat{MOA}+\widehat{AON}\right)=\widehat{xOy}=\alpha\)
\(\Rightarrow\widehat{MON}=2\alpha\)
A