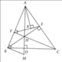
Cho tam giác ABC nhọn AB < AC và các đường cao BE, CF cắt nhau tại H.
a) Chứng minh: ∆ABE ∽ ∆ACF và AF.AB = AE.AC
b) Chứng minh: FA.FB = FH.FC
c) Đường thẳng qua B và song song với FE cắt AC tại M. Chứng minh rằng: ∆BCF ∽ ∆MBE.
d) Gọi I là trung điểm của BM, D là giao điểm của EI và BC. Chứng minh rằng: ba điểm A, H, D thẳng hàng.


a: XétΔABE vuông tại E và ΔACF vuông tại F có
góc BAE chung
Do đó;ΔABE đồng dạng với ΔACF
Suy ra: AB/AC=AE/AF
hay \(AF\cdot AB=AE\cdot AC\)
b: Xét ΔFHB vuông tại F và ΔFAC vuông tại F có
\(\widehat{FBH}=\widehat{FCA}\)
Do đó;ΔFHB\(\sim\)ΔFCA
Suy ra: FH/FC=FB/FA
hay \(FH\cdot FA=FB\cdot FC\)