Khai triển biểu thức 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


(a + b)4 = (a + b)3(a + b)
= (a3 + 3a2b + 3ab2 + b3 )(a + b)
= a4 + 3a3b + 3a2b2 + ab3 + a3b + 3a2b2 + 3ab3 + b4
= a4 + 4a3b + 6a2b2 + 4ab3 + b4

Sử dụng nhị thức Niuton với a = x, b = - m2
x − m 2 4 = x + ( − m 2 ) 4 = C 4 0 . x 4 + C 4 1 . x 3 . − m 2 + C 4 2 . x 2 . − m 2 2 + C 4 3 . x . − m 2 3 + C 4 4 . − m 2 4 = x 4 − 4 x m 2 3 + 6 x 2 m 4 − 4 x . m 6 + m 8
Chọn đáp án D
Nhận xét: học sinh có thể nhầm khi áp dụng sai công thức để dẫn đến các kết quả A,B và C

(2\(x\) + 3y)2
= (2\(x\) + 3y).(2\(x\) + 3y)
= 4\(x\)2 + 6\(xy\) + 6\(xy\) + 9y2
= 4\(x^2\) + 12\(xy\) + 9y2

\(\left(x^2+2\right)^2\)
\(=\left(x^2\right)^2+2\cdot x^2\cdot2+2^2\)
\(=x^4+4x^2+4\)

\(\left(\dfrac{1}{3}y+3\right)^3=\dfrac{1}{27}y^3+y^2+9y+27\)
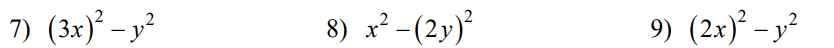
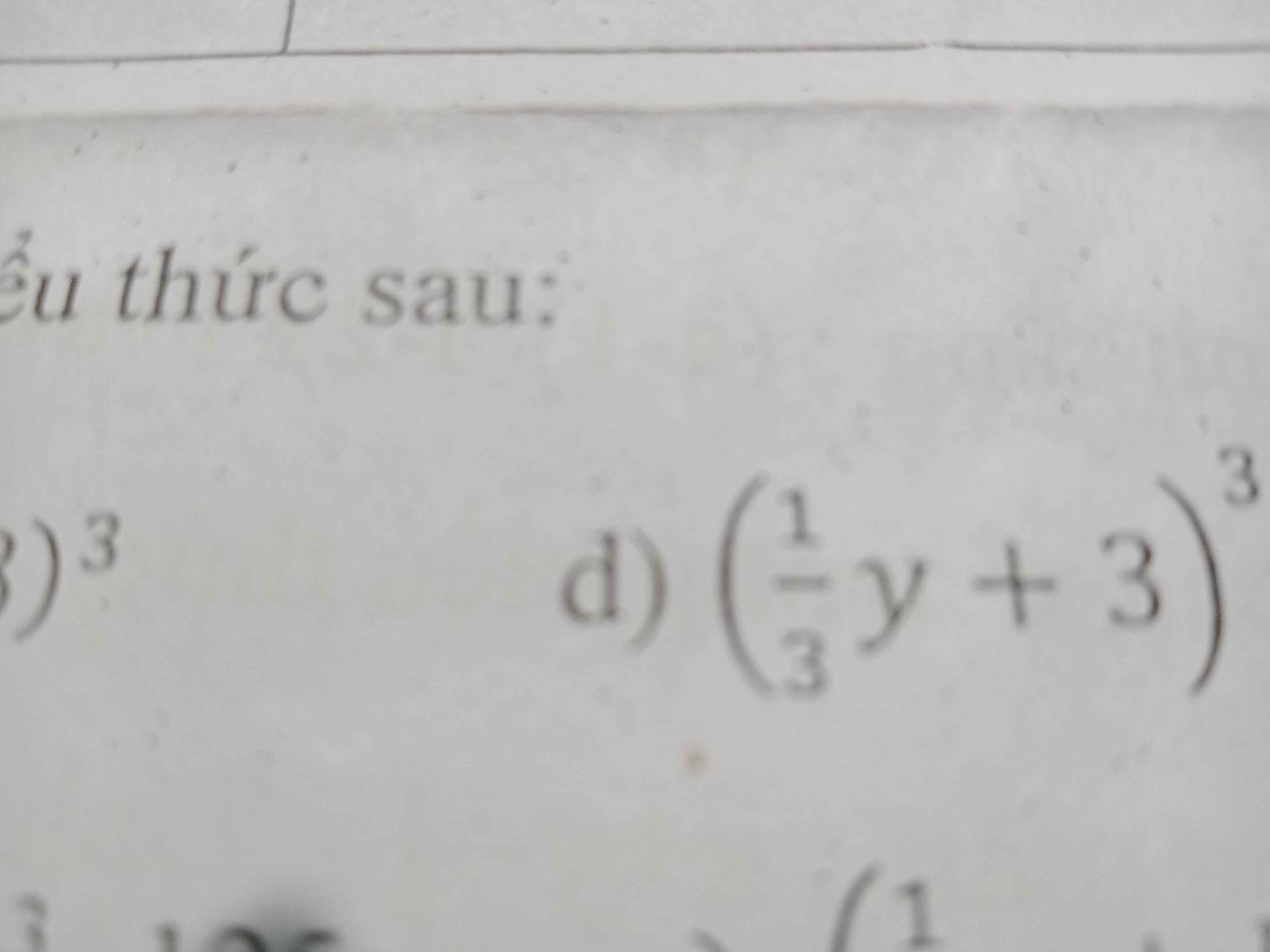
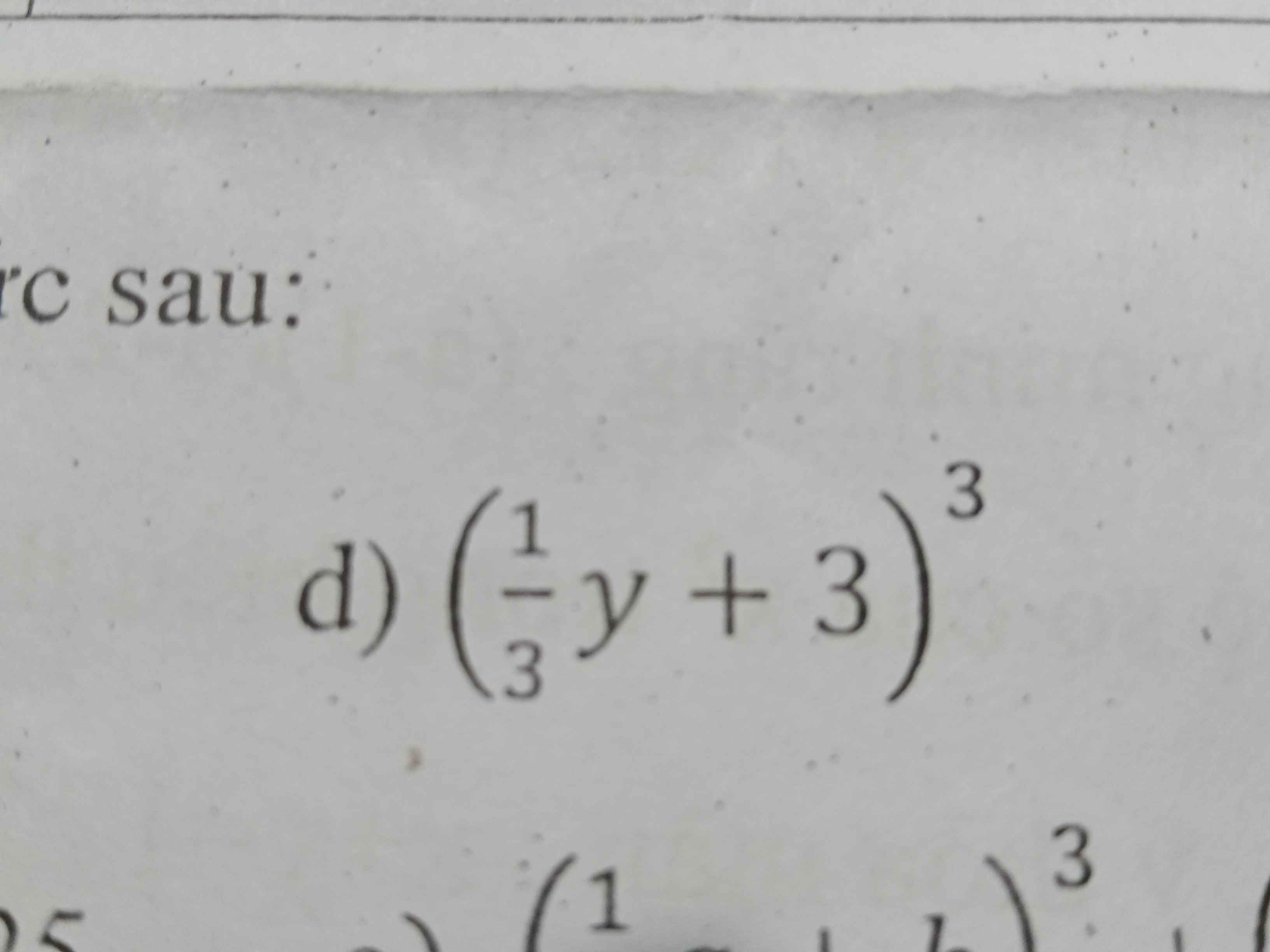
x^3y^6/8 - 27/y^3
= -27x^(3y^6)/(8y^3)
e) \(\frac{x^3y^6}{8}-\frac{27}{y^3}=\left(\frac{xy^2}{2}\right)^3-\left(\frac{3}{y}\right)^3\)
\(=\left(\frac{xy^2}{2}-\frac{3}{y}\right)\left(\frac{x^2y^4}{4}+\frac{3xy}{2}+\frac{9}{y^2}\right)\)