Giải phương trình (x2+16x+60)(x2+17x+60)=6x2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


đặt x2 + 16x + 60 = t thì PT đã cho trở thành :
t ( t + x ) - 6x2 = 0 \(\Leftrightarrow\)t2 + xt - 6x2 = 0
\(\Leftrightarrow\)( t - 2x ) ( t + 3x ) = 0 \(\Leftrightarrow\)\(\orbr{\begin{cases}t=2x\\t=-3x\end{cases}}\)
+) t = 2x thì x2 + 16x + 60 = 2x \(\Leftrightarrow\)x2 + 14x + 60 = 0 ( vô nghiệm )
+) t = -3x thì x2 + 16x + 60 = -3x \(\Leftrightarrow\)x2 + 19x + 60 = 0
\(\Leftrightarrow\)\(\orbr{\begin{cases}x=-4\\x=-15\end{cases}}\)
Vậy ....

Phương trình tương đương với: \(\left(x^2+16x+60\right)\left(x^2+17x+60\right)-6x^2=0.\)
Đặt \(a=x^2+16x+60,\)phương trình trở thành:
\(a\left(a+x\right)-6x^2=0\)
\(\Leftrightarrow a^2+ax-6x^2=0\)
\(\Leftrightarrow\left(a-2x\right)\left(a+3x\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}a-2x=0\\a+3x=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x^2+14x+60=0\\x^2+19x+60=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x^2+2\cdot7\cdot x+7^2-7^2+60=0\\\left(x+4\right)\left(x+15\right)=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}\left(x+7\right)^2+11=0\left(VL\right)\\\left(x+4\right)\left(x+15\right)=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x+4=0\\x+15=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=-4\\x=-15\end{cases}\left(TM\right).}\)
Vậy tập nghiệm phương trình là S = {-15;-4}.

BÀI 1. Giải các phương trình sau bằng công thức nghiệm hoặc (công thức nghiện thu gọn).
1) x2 - 11x + 38 = 0 ;
2) 6x2 + 71x + 175 = 0 ;
3) 5x2 - 6x + 27 =0 ;
4) - 30x2 + 30x - 7,5 = 0 ;
5) 4x2 - 16x + 17 = 0 ;
6) x2 + 4x - 12 = 0 ;

2x3 + 6x2 = x2 + 3x
⇔ (2x3 + 6x2) – (x2 + 3x) = 0
⇔ 2x2(x + 3) – x(x + 3) = 0
⇔ x(x + 3)(2x – 1) = 0
(Nhân tử chung là x(x + 3))
⇔ x = 0 hoặc x + 3 = 0 hoặc 2x – 1 = 0
+ x + 3 = 0 ⇔ x = -3.
+ 2x – 1 = 0 ⇔ 2x = 1 ⇔ x = 1/2.
Vậy tập nghiệm của phương trình là 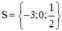

1) Dễ thấy x= 0 không là nghiệm của phương trình nên
P T ⇔ x + 1 x − 1 x + 1 x + 4 = 6
Đặt t = x + 1 x ta được t − 1 t + 4 = 6 ⇔ t 2 + 3 t − 10 = 0 ⇔ t = 2 t = − 5
Với t = 2 ⇒ x + 1 x = 2 ⇔ x 2 − 2 x + 1 = 0 ⇔ x = 1
Với t = − 5 ⇒ x + 1 x = − 5 ⇔ x 2 + 5 x + 1 = 0 ⇔ x = − 5 − 21 2 x = − 5 + 21 2

2x2 – 17x + 1 = 0
Có a = 2; b = -17; c = 1
Δ = b2 – 4ac = (-17)2 – 4.2.1 = 281 > 0.
Theo hệ thức Vi-et: phương trình có hai nghiệm x1; x2 thỏa mãn:
x1 + x2 = -b/a = 17/2
x1.x2 = c/a = 1/2.

6x2-3xy+17x-4y+5=0
⇔ -3xy-4y=-6x2-17x-5
⇔ 3xy+4y=6x2+17x+5
⇔ y(3x+4)=6x2+17x+5
6x2+17x+5 ⋮ 3x-4 vì x, y ∈ Z
⇔ 6x2+17x+12-7 ⋮ 3x+4
⇔ 6x2+8x+9x+12-7 ⋮ 3x+4
⇔ 2x(3x+4)+3(3x+4)-7 ⋮ 3x+4
=> 7 ⋮ 3x+4
=> 3x+4 ∈ Ư(7)={-1,1,-7,7}
3x+4=1 ⇔ x=-1 (lấy)
3x+4=-1 ⇔ x=\(\dfrac{-5}{3}\) (loại)
3x+4=-7 ⇔ x=\(\dfrac{-11}{3}\)(loại)
3x+4=7 ⇔ x=1 (lấy)
thay vào tính thì y={-6,4} (bạn tự làm nhá)
vậy (x,y)={(-1,1),(-6,4)}

`2x^3 +6x^2 =x^2 +3x`
`<=> 2x^3 +6x^2 -x^2 -3x=0`
`<=> 2x^3 +5x^2 -3x=0`
`<=> x(2x^2 +5x-3)=0`
`<=> x(2x^2 +6x-x-3)=0`
`<=> x[2x(x+3)-(x+3)]=0`
`<=> x(2x-1)(x+3)=0`
\(< =>\left[{}\begin{matrix}x=0\\2x-1=0\\x+3=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=0\\x=\dfrac{1}{2}\\x=-3\end{matrix}\right.\)
b)
`(2+x)^2 -(2x-5)^2=0`
`<=> (2+x-2x+5)(2+x+2x-5)=0`
`<=> (-x+7)(3x-3)=0`
\(< =>\left[{}\begin{matrix}-x+7=0\\3x-3=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=7\\x=1\end{matrix}\right.\)
`a) 2x^3 + 6x^2 = x^2 + 3x`
`=> 2x^3 + 6x^2 - x^2 - 3x = 0`
`=> 2x^3 + 5x^2 - 3x = 0`
`=> x(2x^2 + 5x - 3) = 0`
`=> x (2x^2 + 6x - x - 3) = 0`
`=> x [(2x^2 + 6x) - (x+3)] = 0`
`=> x [2x(x+3) - (x+3)] = 0`
`=> x (2x - 1)(x+3) = 0`
`=> x = 0` hoặc `2x - 1 = 0` hoặc `x + 3 = 0`
`=> x = 0` hoặc `x = 1/2` hoặc `x = -3`
`b) (2+x)^2 - (2x-5)^2 = 0`
`=> (2+x+2x-5)(2+x-2x+5) = 0`
`=> (3x - 3)(7-x) = 0`
`=> 3x - 3 = 0` hoặc `7 - x = 0`
`=> x = 1` hoặc `x = 7`

a) 2 x 2 – 17 x + 1 = 0
Có a = 2; b = -17; c = 1
Δ = b 2 – 4 a c = ( - 17 ) 2 – 4 . 2 . 1 = 281 > 0 .
Theo hệ thức Vi-et: phương trình có hai nghiệm x1; x2 thỏa mãn:
x 1 + x 2 = − b / a = 17 / 2 x 1 x 2 = c / a = 1 / 2
b) 5 x 2 – x – 35 = 0
Có a = 5 ; b = -1 ; c = -35 ;
Δ = b 2 – 4 a c = ( - 1 ) 2 – 4 . 5 . ( - 35 ) = 701 > 0
Theo hệ thức Vi-et, phương trình có hai nghiệm x1; x2 thỏa mãn:
x 1 + x 2 = − b / a = 1 / 5 x 1 ⋅ x 2 = c / a = − 35 / 5 = − 7
c) 8 x 2 – x + 1 = 0
Có a = 8 ; b = -1 ; c = 1
Δ = b 2 – 4 a c = ( - 1 ) 2 – 4 . 8 . 1 = - 31 < 0
Phương trình vô nghiệm nên không tồn tại x1 ; x2.
d) 25 x 2 + 10 x + 1 = 0
Có a = 25 ; b = 10 ; c = 1
Δ = b 2 – 4 a c = 10 2 – 4 . 25 . 1 = 0
Khi đó theo hệ thức Vi-et có:
x 1 + x 2 = − b / a = − 10 / 25 = − 2 / 5 x 1 x 2 = c / a = 1 / 25