Cho hình vuông ABCD. Trên cạnh DC lấy điểm E, trên cạnh BC láy điểm F sao cho DE = CF.
Chứng minh rằng AE = DF và \(AE\perp DF\) ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
25 tháng 12 2019
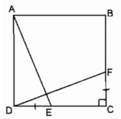
Xét ∆ ADE và ∆ DCF:
AD = DC (gt)
∠ A = ∠ D = 90 °
DE = CF (gt)
Do đó: ∆ ADE = ∆ DCF (c.g.c)
⇒ AE = DF
∠ (EAD) = ∠ (FDC)
∠ (EAD) + ∠ (DEA) = 90 ° (vì ΔADE vuông tại A)
⇒ ∠ (FDC) + ∠ (DEA) = 90 °
Gọi I là giao điểm của AE và DF.
Suy ra: ∠ (IDE) + ∠ (DEI) = 90 °
Trong ∆ DEI ta có: ∠ (DIE) = 180 ° – ( ∠ (IDE) + ∠ (DEI) ) = 180 ° – 90 ° = 90 °
Suy ra: AE ⊥ DF
CM
23 tháng 3 2017
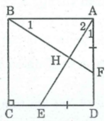
Xét ∆ ABF và ∆ DAE,ta có: AB = DA (gt)
∠ (BAF) = ∠ (ADE) = 90 0
AF = DE (gt)
Suy ra: ΔABF = ΔDAE (c.g.c)
⇒ BF = AE và ∠ B 1 = ∠ A 1
Gọi H là giao điểm của AE và BF.
Ta có: ∠ (BAF) = ∠ A 1 + ∠ A 2 = 90 0
Suy ra: ∠ B 1 + ∠ A 2 = 90 0
Trong ΔABH,ta có: ∠ (AHB) + ∠ B 1 + ∠ A 2 = 180 0
⇒ ( ∠ (AHB) ) = 180 0 – ( ∠ B 1 + ∠ A 2 ) = 180 0 – 90 0 = 90 0
Vậy AE ⊥ BF
D
1
19 tháng 1 2022
Gợi í:)
•Chứng minh cho nó bằng 900 (hoặc đường trung tuyến đồng thời là đường phân giác)
31 tháng 7 2015
a) Xét tam giác ABD và EBD có:
- AB=BE (gt)
- góc ABD = góc EBD ( BD là phân giác góc B)
- Chung cạnh BD
=> Tam giác ABD = tam giác EBD (c.g.c)
=> DA = DE ( 2 cạnh tương ứng)
27 tháng 7 2023
a: góc FEB+góc FBE=45+45=90 độ
=>EF vuông góc BC
b: ΔDFC vuông tại F có góc C=45 độ
nên ΔDFC vuông cân tại F
=>FD=FC
c: Xét ΔBEC có
EF,CA là đường cao
EF cắt CA tại D
=>D là trực tâm
=>BD vuông góc CE
\(\Delta ADE=\Delta DCF\left(c-g-c\right)\), suy ra AE = DF và \(\widehat{DAE}=\widehat{CDF}.\)
Ta lại có \(\widehat{CDF}+\widehat{ADF}=90^o\) nên \(\widehat{DAE}+\widehat{ADF}=90^o.\) Do đó
AE \(\perp\) DF.