Cho hình vuông DEBC. Trên cạnh CD lấy điểm A, trên tia đối của tia DC lấy điển K, trên tia đối của tia ED lấy điểm M sao cho CA = DK = EM. Vẽ hình vuông DKIH (H thuộc cạnh DE).
Chứng minh rằng ABMI là hình vuông ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

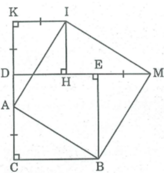
* Xét ∆ CAB và ∆ EMB, ta có:
CA = EM (gt)
∠ (ACB) = ∠ (MEB) = 90 0
CB = EB (tính chất hình vuông)
Suy ra: ∆ CAB = ∆ EMB (c.g.c)
⇒ AB = MB (1)
Ta có: AK = DK+ DA
CD = CA + AD
Mà CA = DK nên AK = CD
* Xét ∆ CAB và ∆ KIA, ta có:
CA = KI (vì cùng bằng DK)
∠ C = ∠ K = 90 0
CB = AK (vì cùng bằng CD)
Suy ra: ∆ CAB = ∆ KIA (c.g.c)
⇒ AB = AI (2)
Ta có: DH = DK (vì KDHI là hình vuông)
Và EM = DK (gt)
Suy ra: DH = EM
⇒ DH + HE = HE + EM
Hay DE = HM
* Xét ∆ HIM và ∆ EMB, ta có: HI = EM (vì cũng bằng DK)
∠ H = ∠ E = 90 0
HM = EB (vì cùng bằng DE)
Suy ra: ∆ HIM = ∆ EMB (c.g.c)
⇒ IM = MB (3)
Từ (1) , (2) và (3) suy ra: AB = BM = AI = IM
Tứ giác ABMI là hình thoi.
Mặt khác, ta có ∆ ACB = ∆ MEB (chứng minh trên)
⇒ ∠ (CBA) = ∠ (EBM)
Mà ∠ (CBA) + ∠ (ABE) = ∠ (CBE) = 90 0
Suy ra: ∠ (EBM) + ∠ (ABE) = 90 0 hay ∠ (ABM) = 90 0
Vậy tứ giác ABMI là hình vuông.

Áp dụng đĩnh nghĩa và giả thiết của hình vuông ABCD, ta được
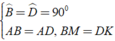
⇒ Δ ABM = Δ ADK ( c - g - c )
Áp dụng kết quả của hai tam giác bằng nhau và giả thiết, ta có:
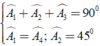
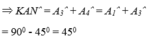

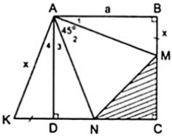
a) Áp dụng đĩnh nghĩa và giả thiết của hình vuông ABCD, ta được
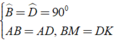
⇒ Δ ABM = Δ ADK ( c - g - c )
Áp dụng kết quả của hai tam giác bằng nhau và giả thiết, ta có:
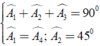
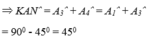

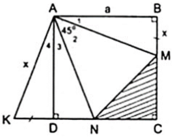
a) Áp dụng đĩnh nghĩa và giả thiết của hình vuông ABCD, ta được
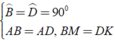
⇒ Δ ABM = Δ ADK ( c - g - c )
Áp dụng kết quả của hai tam giác bằng nhau và giả thiết, ta có:
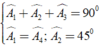
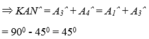

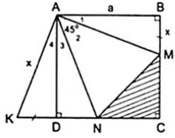
Áp dụng đĩnh nghĩa và giả thiết của hình vuông ABCD, ta được
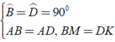 ⇒ Δ ABM = Δ ADK ( c - g - c )
⇒ Δ ABM = Δ ADK ( c - g - c )
Áp dụng kết quả của hai tam giác bằng nhau và giả thiết, ta có:
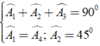
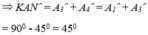

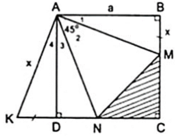
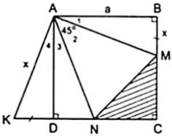
Đặt BM = DK = x thì KN = x + DN, MC = a - x, CN = a - DN
Từ kết quả của hai tam giác bằng nhau ở câu a và giả thiết ta có:
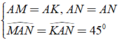 ⇒ Δ AMN = Δ AKN ( c - g - c )
⇒ Δ AMN = Δ AKN ( c - g - c )
⇒ MN = KN (cạnh tương ứng bằng nhau)
Khi đó, chu vi của tam giác MCN là
MC + CN + MN = a - x + a - DN + x + DN = 2a.

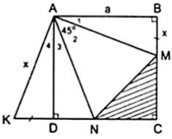
Đặt BM = DK = x thì KN = x + DN, MC = a - x, CN = a - DN
Từ kết quả của hai tam giác bằng nhau ở câu a và giả thiết ta có:
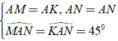 ⇒ Δ AMN = Δ AKN ( c - g - c )
⇒ Δ AMN = Δ AKN ( c - g - c )
⇒ MN = KN (cạnh tương ứng bằng nhau)
Khi đó, chu vi của tam giác MCN là
MC + CN + MN = a - x + a - DN + x + DN = 2a.
Chứng minh các tam giác vuông ACB, IKA, IHM, MEB bằng nhau để suy ra AB = IA = IM = MB. Sau đó chứng minh \(\widehat{IAB}=90^0\)