Giải thích tại sao AD<BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,\dfrac{a}{b}=\dfrac{ad}{bd}\) và \(\dfrac{c}{d}=\dfrac{bc}{bd}\). Do \(\dfrac{a}{b}< \dfrac{c}{d}\) nên \(\dfrac{ad}{bd}< \dfrac{bc}{bd}\).
Suy ra \(ad< bc\)
\(b,\dfrac{a}{b}< \dfrac{c}{d}\) suy ra \(ad< bc\). Do đó \(ab+ad< ab+bc\) nên \(a\left(b+d\right)< b\left(a+c\right)\)
Vậy \(\dfrac{a}{b}< \dfrac{a+c}{b+d}.\) Từ \(ad< bc\) ta cũng có \(ad+cd< bc+cd\) nên \(\left(a+c\right)d< \left(b+d\right)c\)
\(\Rightarrow\dfrac{a+c}{b+d}< \dfrac{c}{d}\)

Vì :
\(\frac{a}{b}=\frac{c}{d}\Rightarrow ad=bc\) (nhân chéo)
Ta có :
\(ab=cd\)
\(\Rightarrow a:d=b:c\)
\(\Rightarrow\frac{a}{b}=\frac{c}{d}\) ( đpcm )

b) Sửa đề: AI là tia phân giác của \(\widehat{A}\)
Xét ΔABI vuông tại I và ΔACI vuông tại I có
AB=AC(ΔABC cân tại A)
AI chung
Do đó: ΔABI=ΔACI(Cạnh huyền-cạnh góc vuông)
Suy ra: \(\widehat{BAI}=\widehat{CAI}\)(hai góc tương ứng)
mà tia AI nằm giữa hai tia AB,AC
nên AI là tia phân giác của \(\widehat{BAC}\)(đpcm)
a) Ta có: AB=AC(ΔABC cân tại A)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)
mà d là đường trung trực của BC(gt)
nên A\(\in\)d

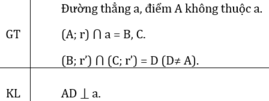
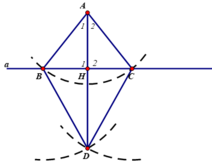
Gọi bán kính cung tròn tâm A là r, bán kính cung tròn tâm B và C là r’.
Xét ΔABD và ΔACD có:
AB = AC (=r)
DB = DC (=r')
AD cạnh chung
Nên ΔABD = ΔACD (c.c.c)
QUẢNG CÁO
- Gọi H là giao điểm của AD và a
ΔAHB và ΔAHC có
AB = AC (= r)
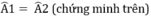
AH cạnh chung
⇒ ΔAHB = ΔAHC (c.g.c)

Hạ BE \(\perp CD\)
Khi đó tính đc: \(\widehat{BED}=90^o\)
\(\Rightarrow\) Hình ABED có dạng hình chữ nhật (hình vuông)
=> AD = BE
Do \(BE\perp CE\)
\(\Rightarrow BE< BC\)
\(\Rightarrow AD< BC.\)