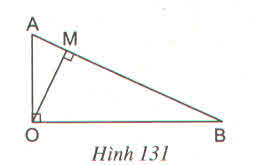
Cho tam giác AOB vuông tại O với đường cao OM (h.131). Hãy giải thích vì sao ta có đẳng thức :
AB . OM = AO .OB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
25 tháng 5 2018
Ta có cách tính diện tích ΔAOB với đường cao OM và cạnh đáy AB:
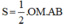
Ta lại có cách tính diện tích ΔAOB vuông với hai cạnh góc vuông OA, OB là:
29 tháng 12 2018
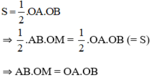
câu 2
Dựng AH là đường cao của ΔABC, khi đó ΔABM,ΔAMC chung chiều cao AH. Ta có:
SAMB=12BM.AH
SAMC=12CM.AH
mà BM=CMBM=CM (vì AM là đường trung tuyến)
Vậy SAMB=SAMC.
S là diện -.-
15 tháng 8 2021
Áp dụng định lí Pytago vào ΔOBA vuông tại O, ta được:
\(AB^2=OA^2+OB^2\)
\(\Leftrightarrow AB^2=R^2+R^2=2R^2\)
hay \(AB=R\sqrt{2}\)
Ta có: ΔOBA vuông tại O
mà OM là đường trung tuyến ứng với cạnh huyền AB
nên \(OM=\dfrac{AB}{2}=\dfrac{R\sqrt{2}}{2}\)
11 tháng 12 2021
\(a,\left\{{}\begin{matrix}OA=OB\\\widehat{AOD}=\widehat{BOD}\left(OD\text{ là p/g}\right)\\OD\text{ chung}\end{matrix}\right.\Rightarrow\Delta OAD=\Delta OBD\left(c.g.c\right)\\ b,\Delta OAD=\Delta OBD\Rightarrow\widehat{ODA}=\widehat{ODB}\\ \text{Mà }\widehat{ODB}+\widehat{ODA}=180^0\\ \Rightarrow\widehat{ODB}=\widehat{ODA}=90^0\\ \Rightarrow OD\bot AB\)
19 tháng 4 2023
1: góc AMO+góc ANO=180 độ
=>AMON nội tiếp
2: ΔOAB cân tại O
mà OM là đường cao
nên M là trung điểm của AB
ΔOAC cân tại O
mà ON là đường cao
nên N là trung điểm của AC
=>NM là đừog trung bình
=>MN//BC
=>MN//AE
=>AMNE là hình thang cân
=>AM=EN; AN=EM
ΔAHB vuông tại H có HM là trung tuyến
nên HM=AB/2=MA=MB
ΔHAC vuông tại H có HN là trung tuyến
nên HN=AN=CN=AC/2
=>HM=EN; HN=EM
=>HMEN là hình bbình hành
=>K làtrung điểm của MN
=>IK vuông góc MN
=>IK vuông góc BC
3: goc MDE+gó MDH=180 độ
=>góc MDE=góc MBH
=>BMDH nội tiếp
=>góc MDB=góc MHB=góc MBH
=>góc MDB=góc MDE
=>DM là phân giác của góc BDE
3 tháng 7 2023
1: góc AMO+góc ANO=180 độ
=>AMON nội tiếp
2: Gọi giao EO và BC là P
AE//BC
AE vuông góc OE
=>OE vuông góc BC
=>OP vuông góc BC
=>P là trung điểm của BC
AEPH là hình chữ nhật
=>AE=PH
EJ giao BC=J
=>AE=JC
=>JC=HP
=>HJ=PC=BC/2=MN
=>HMNJ là hình bình hành
=>HM//NJ và HM=NJ
=>HM//EN và HM=EN
=>EMHN là hbh
=>K là trung điểm của MN
=>IK vuông góc MN
=>IK vuông góc BC
Ta có cách tính diện tích AOB với đường cao OM và cạnh đáy AB:
S = \(\dfrac{1}{2}\) OM. AB
Ta lại có cacnhs tính diện tích AOB vuông với hai cạnh góc vuông OA, OB là
S = \(\dfrac{1}{2}\) OA.OB
Suy ra AB. OM = OA. OB (2S).