Viết công thức tính thể tích hình lăng trụ, hình chóp ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


+ Thể tích V của khối chóp có diện tích đáy B và chiều cao h là V = Bh/3.
+ Thể tích V của khối lăng trụ có diện tích đáy B và chiều cao h là V = Bh.

Hình hộp chữ nhật
Sxq=(a+b)*2*h
Stp=Sxq+2*a*b
V=a*b*h
Hình lăng trụ đứng:
Sxq=C đáy*h
Stp=Sxq+2*S đáy
V=S đáy*h

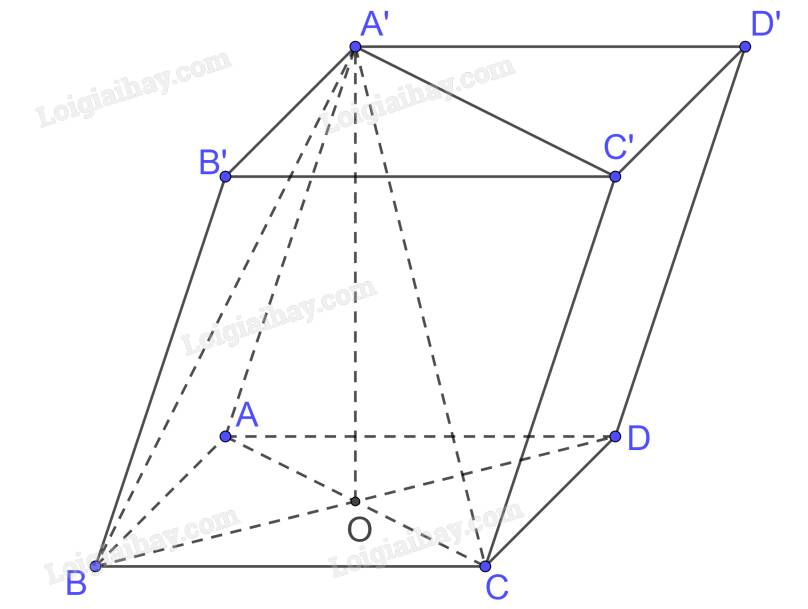
Gọi \(AC \cap BD = \left\{ O \right\}\) mà A’.ABCD là hình chóp đều nên \(A'O \bot \left( {ABCD} \right)\)
Xét tam giác ABC vuông tại B có \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
\( \Rightarrow OA = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}\)
Xét tam giác A’AO vuông tại O có
\(A'O = \sqrt {A{{A'}^2} - A{O^2}} = \sqrt {{a^2} - {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} = \frac{{a\sqrt 2 }}{2}\)
\({S_{ABCD}} = {a^2}\)
Vậy khối lăng trụ có thể tích \(V = \frac{1}{3}A'O.{S_{ABCD}} = \frac{1}{3}.\frac{{a\sqrt 2 }}{2}.{a^2} = \frac{{{a^3}\sqrt 2 }}{6}\)
Nếu hình lăng trụ \(ABCD.A'B'C'D'\) xoay lại thành hình lăng trụ AA’D’D.BB’C’C thì thể tích không thay đổi do đó thể tích hình chóp \(A'.BB'C'C\) bằng một phần 3 thể tích hình lăng trụ AA’D’D.BB’C’C vì chung đáy và chung chiều cao kẻ từ A’ xuống đáy BB’C’C.
Thể tích khối chóp là \({V_{A'.BB'C'C}} = \frac{1}{3}.\frac{{{a^3}\sqrt 2 }}{6} = \frac{{{a^3}\sqrt 2 }}{{18}}\)

Công thức tính thể tích hình lăng trụ đứng là: V = S.h
Đáp án cần chọn là: A

Gọi S là diện tích đáy và h là chiều cao của hình lăng trụ và của hình chóp, ta có:

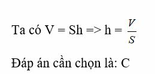
Thể tích hình lăng trụ: V = S . h (Trong đó S là diện tích đáy của hình và h là chiều cao)
Thể tích hình chóp: \(V=\dfrac{1}{3}Sh\)